Huffman编码和Huffman树

1. Huffman编码

2. 前缀编码: 是指对字符集进行编码时，要求字符集中任一字符的编码都不是其它字符的编码的前缀。

   都对应叶结点。
   

3. 树的带权路径长度(WPL)：一定唯一，但是构造的哈夫曼树不一定唯一。

   WPL = 所有叶结点值乘它的路径长度之和。
   

4. 构造过程

   每次选择权值最小的两个点，合并一个树，从下往上构造，最终变成一棵树。
   
   编码：一般情况下，左分支标0、右分支标1，从根结点走到叶结点的路径即为那个叶结点的编码。
   
   （也有左1右0的编码，少，视具体情况分析）
   

1. Huffman树

2. 性质：

   • 所有非叶结点度不为1
   • 一定存在一个最优解，使权值最小的两个点互为兄弟

考题：

2012-41、2013-4、2014-6、2015-3、2017-6、2018-5、2019-3、2020-42

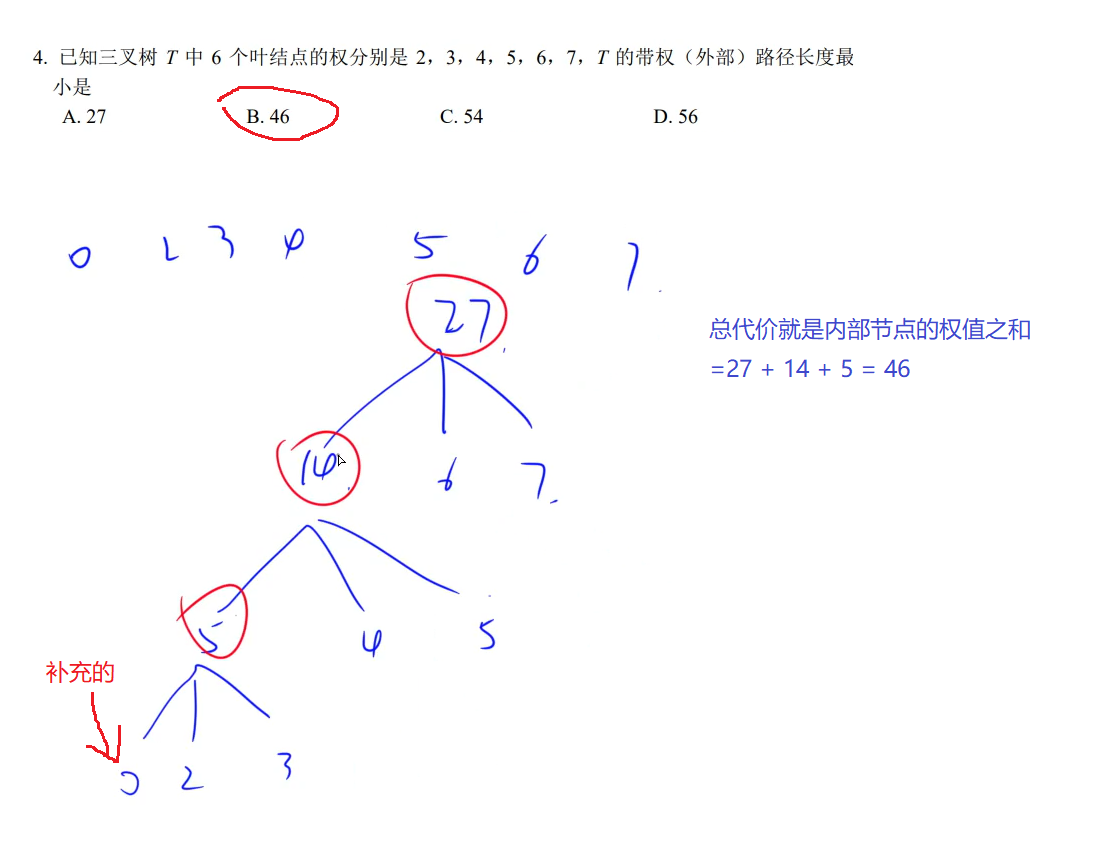
1. 2013-4： n = 6 （点数） ， k = 3 （分叉数）。

(n - 1 ) / (k - 1 ) = 5 / 2 不能整除，所以补一个权值为0的结点才能构建出哈夫曼树。（权值0的不影响结果）

补完后：6 / 2 可以整除就可以构建。

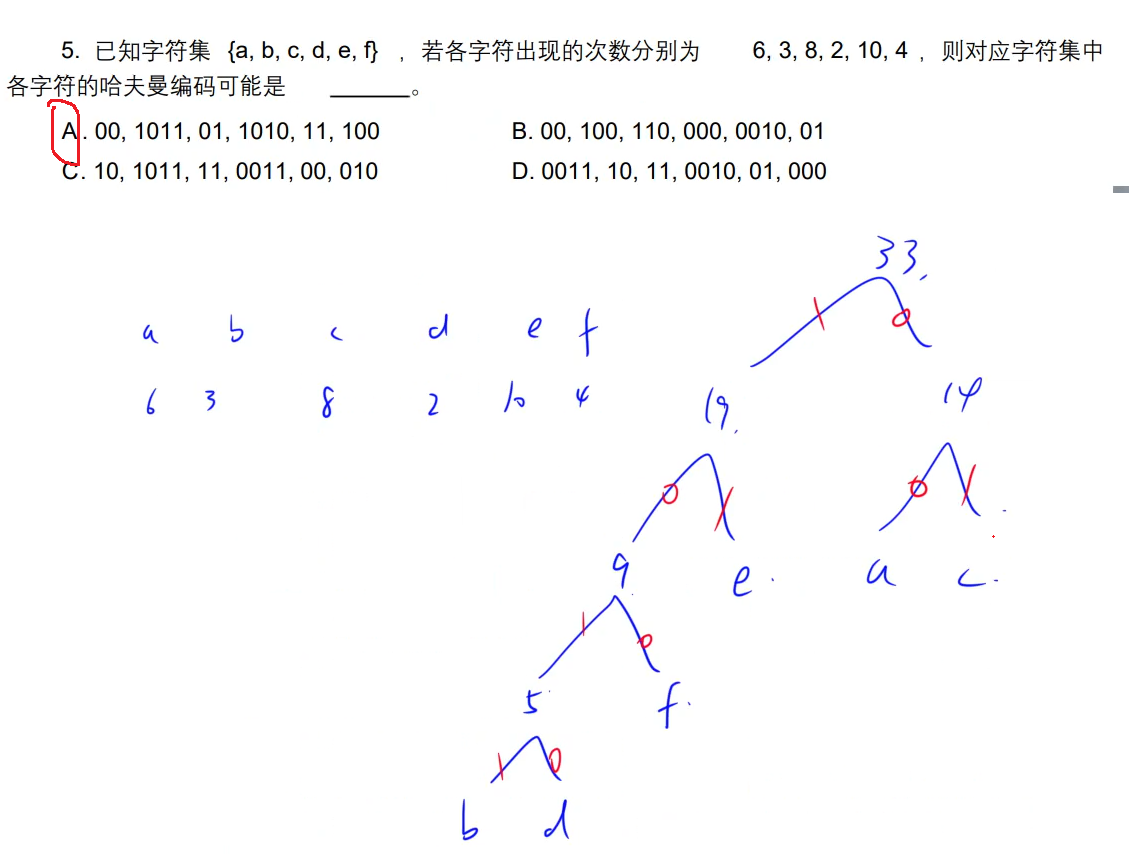
1. 2018-5：哈夫曼的编码不一定都是按照统一的左0右1来构建。如本题（会发现没有规律，有左0右1的，也有左1右0的），只要编码方式不冲突，以及每个字符的长度能够到叶结点即可。