目录传送门

3.6 定点数除法

一、手工除法运算

可以发现除法运算可以通过减法来实现；
但是在运算过程中， 除数要位移多次，且需要$2*n$位的余数寄存器，还需要判断每步是否够减；

二、原码恢复余数除法

如何判断余数是否够减：

通过减法作差，判断差值的符号位即可；

差值为正数则够减，商上1，余数左移一位，再与除数做减法比较；(在手工计算中每次除数右移再进行接下来的运算，这里改进为每次被除数左移，余数就是下一次计算的被除数，两者等效)

差值为负数则不够减，商上0，由于减完之后才判断出来不能减，所以要再加上除数再恢复到原来的值，再将余数左移一位，再与除数做减法比较；（有一个恢复余数的过程）

重复上述过程，知道商达到需要的位数为止；

例如：

已知$X = 0.1001， Y = -0.1011$， 用原码一位除法求$X / Y$;

$[X]_原 = 0.1001，[|X|]_补 = 0.1001$
$[Y]_原 = 1.1011, [|Y|]_补 = 0.1011, [-|Y|]_补 = 1.0101$
（因为需要做减法，所以要求$[-|Y|]补$）

当商的位数达到和被除数位数相同的时候停止除法运算；
除法的符号计算和原码一位乘法相同，要单独计算；
在运算过程中，最后一个上商位直接左移到商中构成除法结果；
除法最终得到的余数是左移了四位的余数，因此真正的余数还要乘以$2^{-4}$;

所以最终答案： $商 = 1.1101， 余数 = 0.0001 * 2^{-4}$;

该方法存在的不足： 运算步数不确定（恢复余数导致运算步数不确定，因为我们实现不知道每一次减法够不够减，步数不确定会对除法控制电路设计带来困难）

三、原码加减交替除法运算方法（不恢复余数法）

设某次运算的余数为Ri，除数为Y，将Ri左移一位然后减除数进行比较上商，即：

$2 * R_i - Y $

恢复余数方法：
当上述结果小于0时，商上0，恢复余数，然后左移一位，减除数作比较，即：

$（2 * R_i - Y） + Y = 2 R_i$
$2 * 2R_i - Y = 4 R_i - Y$

不恢复余数法：

若结果小于0，商上0，不恢复余数而直接将余数左移一位，再加Y：

$（2 * 2R_i - Y） + Y = 4 R_i - Y$

可以发现两种方法最后的结果是一样的，但是不恢复余数法少了恢复余数的步骤；

使用不恢复余数法再对上述例题进行计算：

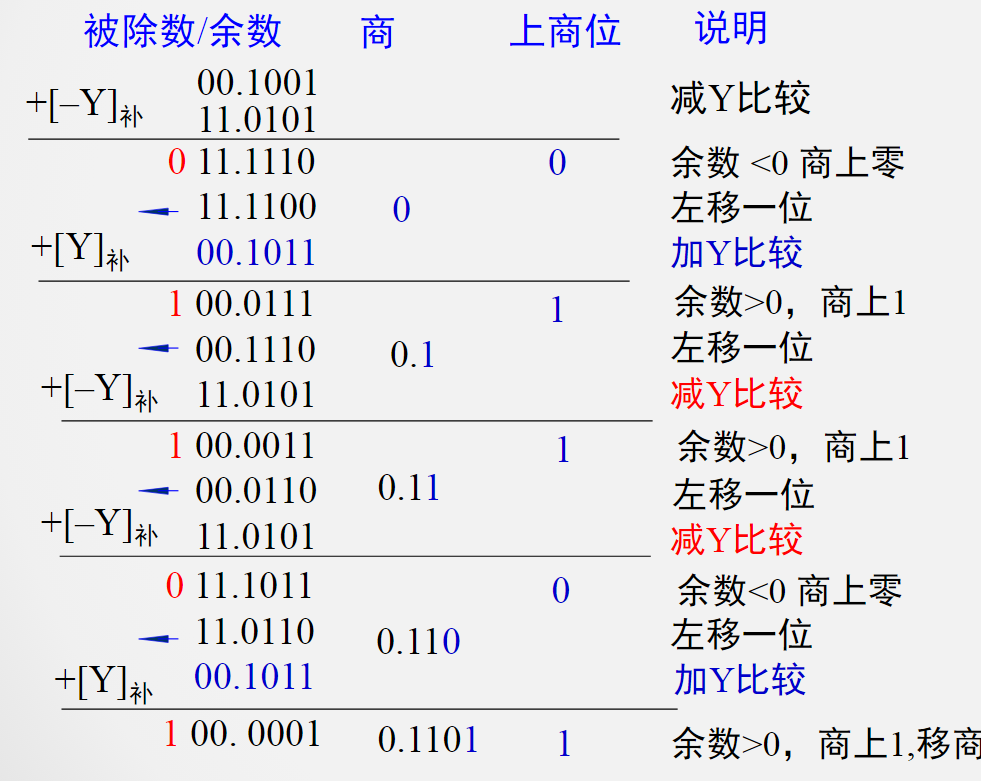
采用不恢复余数法做除法运算使得计算的步数固定了；

四、原码加减交替除法实现逻辑

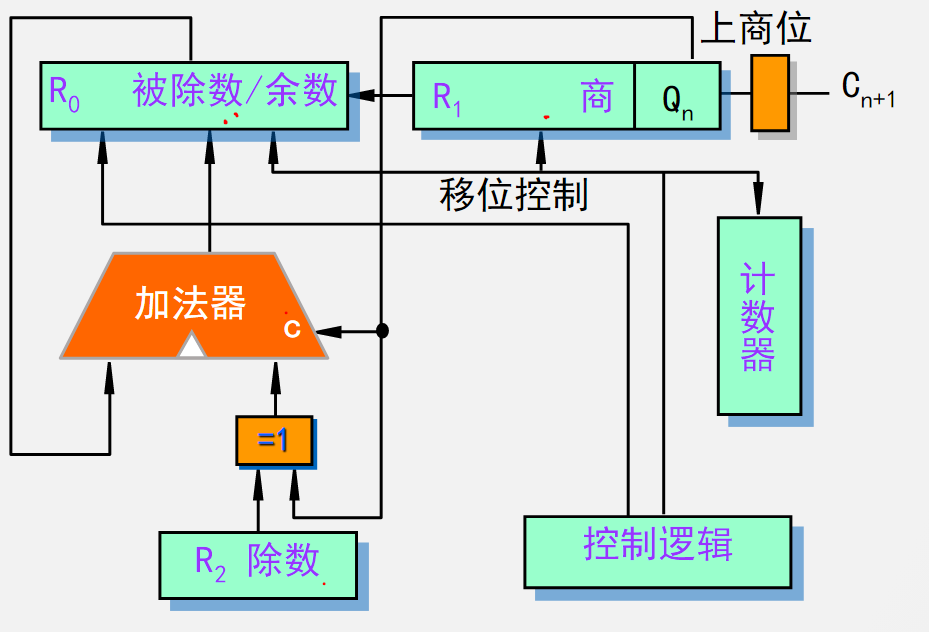
图示说明：

• 不恢复余数法实现除法本质是加法和减法的交替操作，加法由余数来控制，因此除法电路要有加法器；

• 被除数和余数在同一个地方存放，因为余数是下一次运算的被除数；

• 移位控制控制左移；

• 观察不恢复余数法的计算过程，发现上商位的值其实就是每一步加法运算的进位位，因此加法器的进位输出位就是上商位的驱动；

• 随着左移的进程，上商位移动到了商寄存器的最低位，又由最低位控制下一步运算作加法还是减法；（当商寄存器最低位为1时，除数会进行取反加一操作，等效于变为减法）

五、阵列除法

（1）可控加法/减法(CAS)单元

运算单元如图所示：

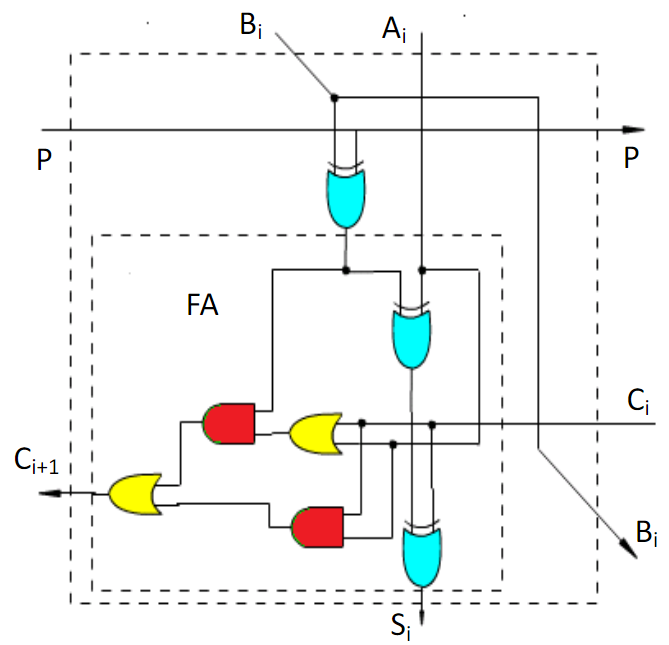
内层虚线框就是一个加法器电路；
外层虚线框是对加法器的一个改进电路；

$CAS$单元的输入与输出的关系可用如下一组逻辑方程来表示：

$S_i ＝ A_i⊕(B_i⊕P)⊕C_i$

$C_i ＋ 1 ＝ (A_i＋C_i)·(B_i⊕P)＋A_iC_i $

当$P = 0$时，逻辑表达式等效于作加法运算；
当$P = 1$时，逻辑表达式等效于作减法运算；

P其实就是做加法还是减法的控制信号；

（2）基于CAS的阵列除法

除法阵列如图示：

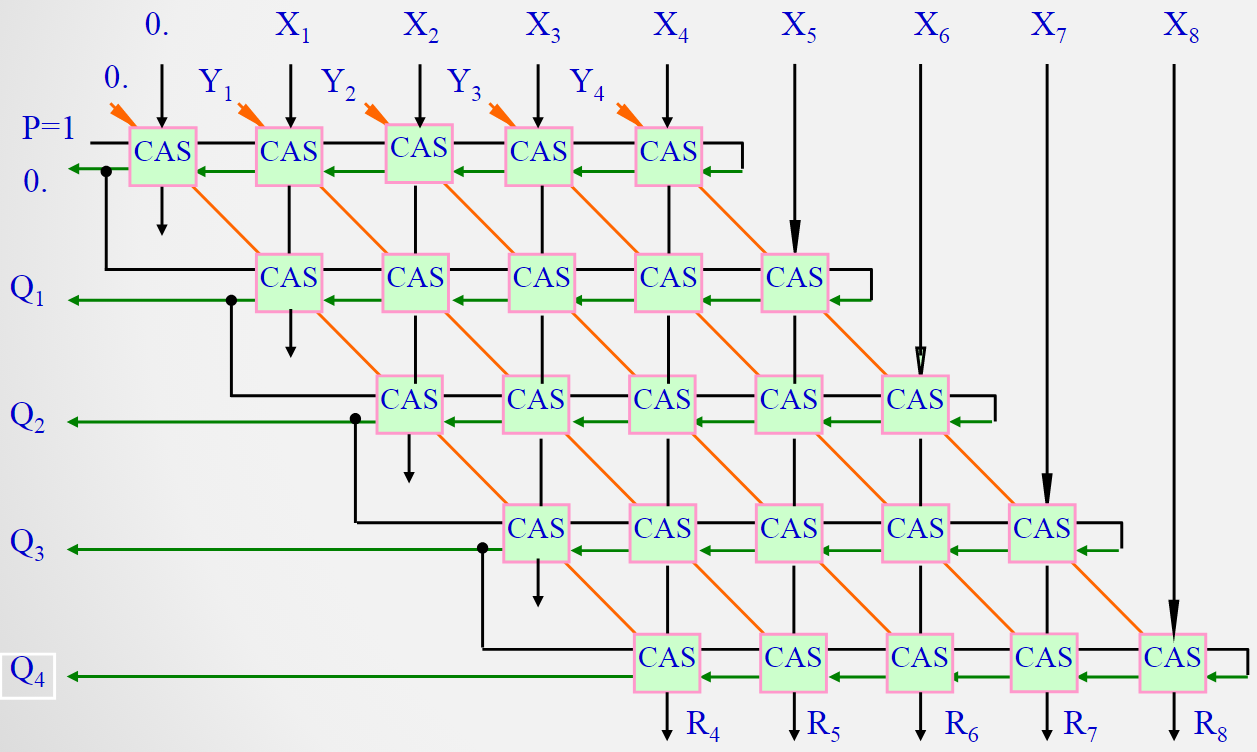
由于第一步操作一定是试商，因此第一步一定是减法操作，P一开始为1；

每一次操作是否要执行加法，是由上一步操作的上商位决定的，因此每一次上商的结果要连到下一轮除法运算电路中作为控制信号；

以此类推，即可得到满足位数要求的际遇CAS的阵列除法器；

除数结果为左侧的Q1 ~ Q4，余数结果为每一位竖线的输出；

每执行完一步除法，就将除数右移1位(原理同手工除法，要和循环除法器的左移操作区别开)