第二章 条件概率
上一章已经介绍了概率是一种表达不确定性的语言. 每当观察一个新的现象时(获取新数据), 新获取的信息
可能会影响我们对不确定性的判断 :
- 与现有判断一致的新观察会使人们更加肯定原有的判断.
- 一个意想不到的观测结果会使人们对原有的判断产生怀疑.
条件概率(conditionnal probability)用于解决一个问题 :
- How should you update your
probability/belief/uncertaintybased on new evidence in a coherent,
consistent, logical way. - 如何基于新数据以一种连贯, 一致, 合乎逻辑的方式更新你的
概率/信念/不确定性.
2.1 条件思考的重要性
条件概率对于科学, 医学以及法律推理是至关重要的, 因为它说明了如何以合乎逻辑且相一致的方式将证据
纳入人们对世界的理解当中. 事实上, 有观点认为所有的概率都是有条件的, 无论是否明确标出, 每个概率
都有背景(或假设)存在.
例子
例如, 假设一天早上, 张三被发现惨死家中, 福尔摩斯先生来到现场, 我们先设事件T:张三是被他杀;
如果后来发现窗户有被破坏的痕迹, 此时福估计T发生的概率程度上升; 将新概率表示为$P(T\mid W)$(读作
"给定W发生的条件下, T发生的概率"), 这里W表示事件窗户被破坏.
随着时间推移, 默尔摩斯会观察到$B_1, …, B_n$发生, 那么可以马上写出更新的条件概率$P(R\mid B_1,…,B_n)$
当福尔摩斯排除所有可能后, 最终会判断条件概率为1或0.
此外, 添加条件也是一种非常有效的解决问题的策略. 通过把复杂问题分解为一个个相互独立且容易解决的
小问题, 然后逐个分析解决, 以解决复杂的问题. (类似分治算法, 分而治之).
Conditioning is the soul of statistics. 条件概率是统计学的灵魂.
2.2 定义和直观解释
定义 2.2.1 条件概率
若$A$和$B$为事件, 且$P(B)\gt 0$, 那么给定事件$B$, 事件$A$的条件概率用$P(A\mid B)$表示, 定义如下
$\;\; P(A\mid B) = \frac{P(A\cap B)}{P(B)}$.
这里事件$A$是观测到事件$B$发生前的概率, 事件$B$是观测到的证据(或者视为给定条件), $P(A)$称作$A$的
先验概率, $P(A\mid B)$是$A$的后验概率. (基于证据$B$的更新前/后)
过程 – $P(A)$:不知道$B$是否发生-->观察到$B$发生了! --> 更新此时$A$发生的概率为$P(A\mid B)$.
重要的是将竖线后的事件解释为人们已经观察到或正在被条件化的证据 : $P(A\mid B)$是给定证据$B$后(即$B$
已经发生), $A$的概率, 并不是一个叫做$A\mid B$的事件的概率, 不存在事件$A\mid B$.
对任意事件$A$, $P(A\mid A) = P(A\cap A)/P(A) = 1$. 在观测到$A$发生后, 其概率更新为1. 如果事实不是
这样, 那么我们就需要对这一条件概率重新进行定义!
例2.2.2 两张牌
洗好一副标准扑克后, 从中随机抽取两张, 无放回地一次抽一张. 设事件$A$表示第1一张牌为红桃, 事件B表示
第2张为红色. 求$P(A\mid B)$和$P(B\mid A)$.
解:
由概率朴素定义和乘法法则, 有
$\;\; P(A\cap B) = \frac{12 * 25}{52 * 51} = \frac{25}{204}$
第一次从13张红桃中选择, 第二次从剩下的25张牌中选择. 由于4种花色概率相同, 所以$P(A)=1/4$, 且
$\;\; P(B) = \frac{26 * 51}{52 * 51} = \frac{1}{2}$
因为对于第二张牌有26种选择, 第一张牌有51种选择(乘法法则不一定要按照时间顺序). 一种更简洁的方法
是通过对称性得到$P(B) = 1/2$ : 总体来看, 在实施实验前, 第二张牌是所有牌种的任意一张且可能性均等.
现在我们已经具备了应用条件概率定义所需的所有内容 :
$\;\; P(A\mid B) = \frac{P(A\cap B)}{P(B)} = \frac{25/204}{1/2} = \frac{25}{102}$
$\;\; P(B\mid A) = \frac{P(A\cap B)}{P(A)} = \frac{25/204}{1/4} = \frac{25}{51}$
注意
上述是一个简单案例, 还有几点是需要注意的.
-
注意哪些事件放在竖线$\mid$的哪一边是很重要的. 具体来说$P(A\mid B) \not= P(B\mid A)$, 接下来将探究两者
是如何联系起来的. 如果将这两个变量混淆则称为检察官谬误(prosecutor's fallacy), 将在2.8节讨论. -
无论$P(A\mid B)$还是$P(B\mid A)$都是有意义的(直观上或数学上); 牌抽取的事件顺序不能决定出现何种条件
概率 在计算条件概率时, 我们考虑的是一个事件给另一个事件带来的信息, 而不是一个事件是否导致另一个事件发生. -
此外, 可以通过条件概率的直接解释得出$P(B\mid A) = 25/51$ : 给定第一张抽的牌是红桃, 那么剩下的牌
由25张红色牌和26张黑色牌组成, 所有牌第二次被抽到的可能性相同, 所以抽取的是红色牌的概率是$25/(25+26)=25/51$. 但通过这种方式得到$P(A\mid B)$是很难的, 假设我们知道
第二张牌是红色, 我们还需知道是否是红桃. 本章后面部分给出的条件概率结果提供了解决这个问题的方法.
为了更好的阐明条件概率的意义, 这里有两种直观的解释.
直观解释 2.2.3 圆点/卵石空间 pebble world
考虑一个有限的样本空间, 所有结果可以看作是很多圆点, 总质量为1. $A$, $B$是事件, 所以它们是一些
圆点的集合(subset).
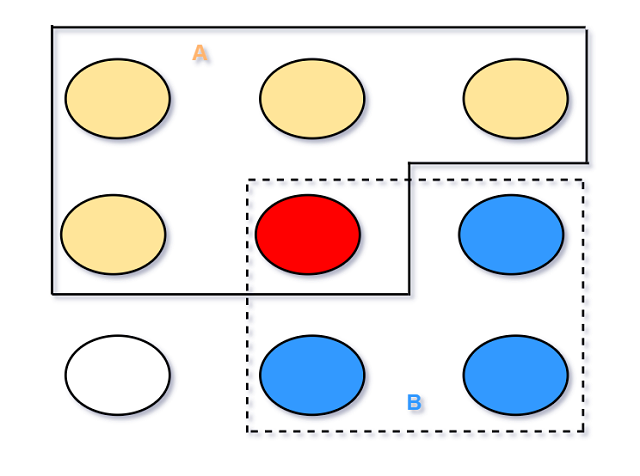
现在假设我们观察到事件$B$发生, 获得此信息后, 将所有在$B^c$的事件剔除, 因为它们与$B$事件已发生这个
事实不符. 这时$P(A\cap B)$就表示所有剩余的且在$A$中的质量.
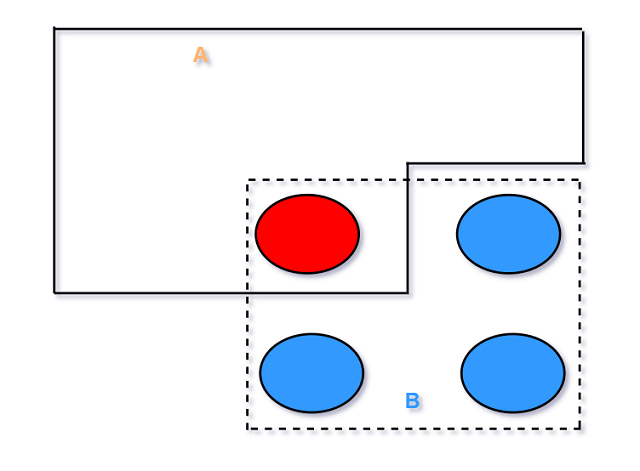
最终, 对已知$B$发生后剩余事件重新归一化(renormalize) : 除以一个常数使得所有留下圆点的
质量和为1.本例中就是除以$B$中所有圆点质量之和$P(B)$. 对事件$A$, 其更新后的结果为
条件概率$P(A\mid B) = P(A\cap B)/P(B)$.
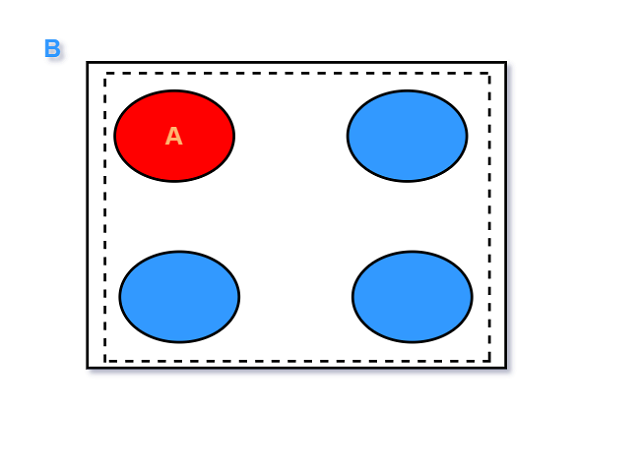
由上述过程, 概率就会根据已经得到的证据进行更新. 剔除与证据相矛盾的结果后, 它们的质量被重新分配到
剩余的结果中, 以总质量(概率)为1且保持剩余结果的相对质量不变.
直观解释 2.2.4 频率解释 frequentist world
回想一下, 概率的频率解释为基于大量重复实验的相对频率. 假设实验重复多次, 生成了一长串结果序列. 可以
通过一种自然的方式思考给定$B$发生时$A$发生的概率: 它表示限制在$B$发生的所有结果中, $A$发生的次数的比例.
上图中实验结果用0个1组成的字符串表示; $B$事件表示第一个字符为1, $A$事件表示第二个字符为1.
以$B$为条件, 先将所有$B$发生的结果圈起来, 然后找被圈结果中$A$发生的比例数。
令$n_A、n_B、n_{AB}$分别表示进行$n$次大量重复实验后$A、B、A\cap B$所发生的次数. 频率解释如下:
$\;\; P(A)\approx \frac{n_A}{n}, P(B)\approx \frac{n_B}{n}, P(A\cap B)\approx \frac{n_{AB}}{n}$.
此时$P(A\mid B) = n_{AB}/n_B$, 正好等于$P(A\cap B)/P(B) = (n_{AB}/n)/(n_B/n)$.
接下来3个有关条件概率的示例都是以一个有两个孩子的家庭为基本场景展开的, 细微之处取决于示例中
分别作为条件的确切信息.
例 2.2.5 年长的是女孩 vs 至少一个是女孩
某家庭有两个孩子, 已知至少有一个是女孩. 两个孩子都是女孩的概率是多少? 如果条件改为年长的是女孩,
那么两个都是女孩的概率是多少?
解:
假设每个孩子是女孩和男孩的可能性相同且不相关(相互独立,之后会正式引入), 那么
$\;\; P(都是女孩\mid 至少有一个是女孩) = \frac{P(都是女孩\cap 至少有一个是女孩)}{P(至少有一个是女孩)}$
= $\frac{P(都是女孩)}{P(至少一个)} = \frac{1/4}{3/4} = 1/3$
$\;\; P(都是女孩\mid 年长的是女孩) = \frac{P(都是\cap 年长)}{P(年长)} = \frac{P(都是)}{P(年长)} = \frac{1/4}{1/2} = 1/2$
一开始看到这个结果似乎是反直觉的 : 对于两个都是女孩我们没有必要关注基于年长还是较小的孩子是女孩.
事实上, 通过对称性可以得到 :
$\;\; P(都是女孩\mid 年轻的是女孩) = P(都是女孩\mid 年长的是女孩) = 1/2$
然而条件概率$P(都是女孩\mid 年长的是女孩)$和$P(都是女孩\mid 至少一个是女孩)$之间没有这样的对称性.
指定一个特定的孩子是女孩会从4个样本{$GG, GB, BG, BB$}中剔除两个, 而至少一个是女孩只会剔除一个
样本$BB$. (B:男孩, G:女孩).
例 2.2.6 随机的一个孩子是女孩
某家庭有两个孩子, 随机遇到其中一个, 发现是女孩. 给定这一信息后, 两个孩子都是女孩的概率是多少? 假设
随机遇到两个孩子的可能性相同, 且与性别无关.
解:
直观来看, 结果应该是$1/2$ : 我们随机碰到的女孩就在面前, 而另一个孩子不在. 两个孩子都是女孩说明在此基础
上另一个孩子是女孩, 且与我们面前的孩子的性别无关, 所以另一个孩子是男孩/女孩的概率为$1/2$.
令$G_1, G_2, G_3$分别表示年长、年幼、随机的孩子是女孩这3个事件. 有对称性可得$P(G_1)=P(G_2)=P(G_3)=1/2$
(这里隐含的假设是, 在不考虑其他任何信息时, 任何一个特定的孩子是男孩还是女孩的可能性相同). 根据朴素
概率定义(或2.5节独立性), $P(G_1\cap G_2) = 1/4$. 因此
$\;\; P(G_1\cap G_2\mid G_3) = P(G_1\cap G_2\cap G_3)/P(G_3) = P(G_1\cap G_2)/P(G_3) = (1/4)/(1/2) = 1/2$
($G_1\cap G_2\cap G_3 = G_1\cap G_2$ : 如果两个孩子都是女孩, 那么随机选取的肯定是女孩).
请记住, 为得出$1/2$这个解, 需要对如何随机选取这个孩子做出假设. 统计学语言中, 称之为收集了一个随机样本.
统计学最重要的原则之一是必须仔细考虑样本是如何收集的, 而不能是只盯着原始数据却不知道它是如何来的.
例如,一个极端例子 : 假设法律规定, 如果一个男孩有姐妹则禁止他走出家门, 那么这时”随机遇到一个女孩”
就等价于”至少有一个女孩”, 此时问题变成了例2.2.5的第一问.
例 2.2.7 冬天出生的女孩
某家庭有两个孩子. 给定条件至少一个是女孩且在冬天出生, 求两个孩子都是女孩的概率. 假设4个季节出生的
可能性相同且性别和季节是相互独立的(已知性别不会给出生季节的概率提供任何信息, 反之亦然).
解:
由条件概率定义,
$\;\; P(两个都是女孩\mid 至少有一个是在冬天出生的女孩) = $
$\;\; \frac{P(两个都\cap 至少一个冬天)}{至少一个冬天}$
由于指定的孩子是在冬天出生的女孩的概率是$1/2\times 1/4 = 1/8$, 所以上式的分母等于:
$\;\; P(至少有一个冬天) = 1 - P(都不是在冬天出生的女孩) = 1 - (7/8)^2$
计算分子时, 事件等价于”两个都是女孩, 至少有一个孩子是在冬天出生的”; 然后利用性别和季节独立的假设:
$\;\;\;\;P(两个都\cap 至少一个女孩冬天) = $
$\;\;\;\;P(两个都, 至少有一个孩子是在冬天出生) = $ /*为方便书写, 下面有时用,等价表示$\cap$*/
$\;\;\;\;(1/4)P(至少有一个孩子是在冬天出生) = $
$\;\;\;\;(1/4)(1 - P(两个孩子都不是在冬天出生)) = $
$\;\;\;\;(1/4)(1-(3/4)^2)$. 所以
$\;\;P(两个都是女孩\mid 至少有一个是在冬天出生) = \frac{(1/4)(1-(3/4)^2)}{1-(7/8)^2} = 7/15$
一开始这个我们可能会觉得结果很荒谬, 里2.2.5中已经看到给定至少有一个是女孩的前提下,
两个都是女孩的概率是$1/3$; 为什么我们知道至少有一个是在冬天出生的女孩后, 概率会有所不同? 关键点在于,关于出生季节的信息使得”至少有一个是女孩”解决于指定其中一个孩子是女孩. 条件中越来越多的指定信息使得概率越来越接近于$1/2$.
例如, 条件”至少有一个是女孩且在3月31号晚上8:00出生就非常接近于指定一个孩子, 且这个指定孩子的
信息不会提供另一个的信息(相互独立). 看似不相关的信息(如出生季节), 使得概率处于例2.2.5的两个问题的
概率之间.
2.3 贝叶斯准则和全概率公式
Thinking conditionally is condition for thinking.
条件概率 : $P(A\mid B) = \frac{P(A\cap B)}{P(B)}$
可以通过将定义中的分母移动到另一侧得到:
定理 2.3.1 交的概率
对于任意两个概率为正(分母大于0)的事件$A$和$B$, 有
$\;\;\;\; P(A\cap B) = P(B)P(A\mid B) = P(A)P(B\mid A)$
上式可以直接由代数得出, 对条件概率的形式做了一点变化, 在某些情况下可以求交的概率.
$A, B$同时发生的概率 = $B$发生概率$\times $$A$在$B$发生条件下的概率 = …
重复运用定理2.3.1, 可以将其推广到n个事件的交集.
定理 2.3.2 n个事件的交
对于任意的正概率事件$A_1, A_2, …, A_n$, 有
$\;\;\;\; P(A_1, A_2, …, A_n) = P(A_1)P(A_2\mid A_1)P(A_3\mid A_1,A_2)…P(A_n\mid A_1,…,A_{n-1})$
式中的逗号,表示交集.
事实上这是将$n!$个等式合一, 因为我们可以任意排列$A_1, …, A_n$的顺序而不影响等式左边(对称性).
通常存在某些顺序更容易计算.
接下来将介绍本章两大定理, 贝叶斯准则和全概率公式. 贝叶斯准则是将$P(A\mid B)$和$P(B\mid A)$联系在一起的准则.
定理2.3.3 贝叶斯准则
$\;\;\;\; P(A\mid B) = \frac{P(A)P(B\mid A)}{P(B)}$
上式也可直接通过代数得出. 因为通常求$P(A\mid B)$比求$P(B\mid A)$更容易(或者反过来), 所以贝叶斯准则
在概率论和统计中有重要的含义和应用.
另一种贝叶斯准则的表达方式是以几率(odds)的形式写出, 而非概率形式.
定义 2.3.4 几率
一个事件$A$的几率(odds)为 :
$\;\;\;\; odds(A) = P(A)/P(A^c)$
例如, 如果$P(A) = 2/3$, 就称支持$A$的几率比为$2$比$1$. 几率也能转化为概率的形式 :
$\;\;\;\; P(A) = odds(A)/( 1 + odds(A) )$
通过将$P(A\mid B)$的贝叶斯准则表达式除以$P(A^c\mid B)$的贝叶斯准则表达式, 就得到了贝叶斯几率形式:
$\;\;\;\; \frac{P(A\mid B)}{P(A^c\mid B)} = \frac{P(B\mid A)P(A)}{P(B\mid A^c)P(A^c)}$
换句话说, 就是后验几率$P(A\mid B)/P(A^c\mid B)$等于先验几率$P(A)/P(A^c)$乘以因子$P(B\mid A)/P(B\mid A^c)$
这个因子就是统计学中有名的 似然比 . 有时用上述形式可以方便计算后验几率, 需要的化可以再转换为概率形式.
全概率公式能将条件概率和非条件概率联系到一起. 它使得条件概率可以用于将复杂的概率问题分解为更
简单的部分, 经常与贝叶斯准则一起使用.
how to solve a problem
- try simple and extreme cases 尝试简单和边界例子
- break problems into simpler pieces 将问题分解为更简单的部分. 这也是全概率公式的思想.
定理2.3.6 全概率公式 law of total probability
设$A_1, …, A_n$为样本S的一个划分($A_i$彼此不相交且它们的并为$S$), 且对所有$i, P(A_i)\gt 0$, 则有
$\;\;\;\; P(B) = \sum_{i=1}^{n} P(B\mid A_i)P(A_i)$
证明:
因为$A_i$构成了对S的划分, 所以可以将$B$分解为:
$\;\;\;\;B = (B\cap A_1)\cup (B\cap A_2)\cup …\cup (B\cap A_n)$.
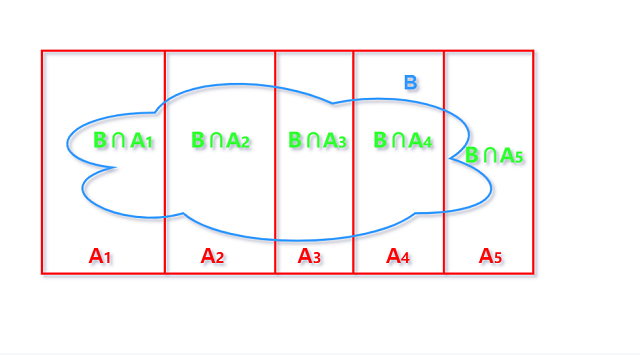
由概率公理2, 因为每个部分均不相交, 所以$B$的概率可以对每部分求和得到 :
$\;\;\;\; P(B) = P(B\cap A_1) + P(B\cap A_2) + … + P(B\cap A_n)$.
我们将定理2.3.1应用到每个$P(B\cap A_i)$上, 得到
$\;\;\;\; P(B) = P(B\mid A_1)P(A_1) + … + P(B\mid A_n)P(A_n)$.
由全概率公式可知, 为了去的$B$的无条件概率, 可以先把样本空间划分为不相交的部分$A_i$, 并找出每个
部分中$B$的条件概率, 然后再以权重$P(A_i)$加权求和. 关键点在于如何划分以使问题分解为简单的部分.
接下来几个例子显示了如何综合使用贝叶斯准则和全概率公式, 以及如何根据观察到的证据来更新确认程度.
例 2.3.7 随机抛硬币
假设有一枚均匀的硬币和一枚以概率$3/4$正面朝上的不均匀硬币. 随机选取一枚硬币抛3次, 3次都是
正面朝上. 给定该信息后, 判断选取的硬币是均匀硬币的概率有多大?
解:
令$A$事件代表选取的硬币3次都是正面朝上, $F$事件表示选取的硬币是均匀的. 我们感兴趣的是$P(F\mid A)$.
但实际上更容易计算的是$P(A\mid F)$和$P(A\mid F^c)$, 因为这是在确定何种硬币的前提下计算. 这也暗示我们
可以使用贝叶斯准则和全概率公式, 有
$\;\;\;\;P(F\mid A) = \frac{P(A\mid F)P(F)}{P(A)}$ //贝叶斯准则
$\quad \quad \quad = \frac{P(A\mid F)P(F)}{P(A\mid F)P(F) + P(A\mid F^c)P(F^c)}$ //全概率公式
$\quad \quad \quad = \frac{(1/2)^3\times (1/2) }{ (1/2)^3\times (1/2) + (3/4)^3\times (1/2)}$
$\quad \quad \quad \approx 0.23$
在掷硬币前, 选取硬币的概率被认为是等可能的, 即$P(F) = P(F^c) = 1/2$. 当观察到3次正面朝上后, 我们
认为选取的硬币是不均匀的可能性更大.
2.3.8 先验 vs 后验 -ω-
在上例第一步计算中, 认为"因为$A$已经发生了, 所以$P(A) = 1$"是不对的. 正确的应该是$P(A\mid A) = 1$.
因为$P(A)$是事件$A$的先验概率, $P(F)$是$F$的先验概率, 两个都是在观察到任何新数据前的概率. 这些不能和
基于条件$A$的后验概率相混淆.
例2.3.9 一种罕见疾病的检测
一位名叫Fred的患者正在检测是否患有一种叫做conditionitis的疾病. 该疾病在人群中的发病率为$1\%$.检测
结果为阳性, 则说明检测结果认为Fred患病. 令事件$D$表示确认Fred有此病, 事件$T$表示检测结果为阳性.
假设检测是"$95\%$准确的", 本题中假设其意味着$P(T\mid D) = P(T^c\mid D^c) = 0.95$. $P(T\mid D)$
也被称为真阳性率(检测患病并确实患病); $P(T^c\mid D^c)$被称为真阴性率(检测没病并确实没病).
给定检测结果为阳性这一条件, 求Fred确实患有此病的概率(即求$P(D\mid T)$).
解:
运用贝叶斯准则和全概率公式, 可以得到
$\;\;\;\; P(D\mid T) = \frac{P(T\mid D)P(D)}{P(T)}$
$\;\;\;\;\; = \frac{P(T\mid D)P(D)}{P(T\mid D)P(D) + P(T\mid D^c)P(D^c)}$
$\;\;\;\;\; = \frac{0.95\times 0.01}{0.95\times 0.01 + (1-0.95)\times 0.99}$
$\;\;\;\;\; \approx 0.16 $
因此, 即使这种检测看上去可信度很高, 但在给定检测结果是阳性的条件下, 也只有$16\%$的概率认为Fred确实
患有此病. 很多人包括医生都惊讶于这个结果. 理解这个后验概率的关键在于意识到这里有2个影响因素 :
检测结果和关于这个疾病的先验概率 : 虽然检测可信度高, 但这是一个罕见疾病! 条件概率$P(D\mid T)$反映
的是对这两个影响因素的权衡, 它恰当的衡量了疾病的罕见性和测试结果错误的稀有性.
为进一步进行直观解释, 考虑一个10000人组成的群体, 其中100患病.
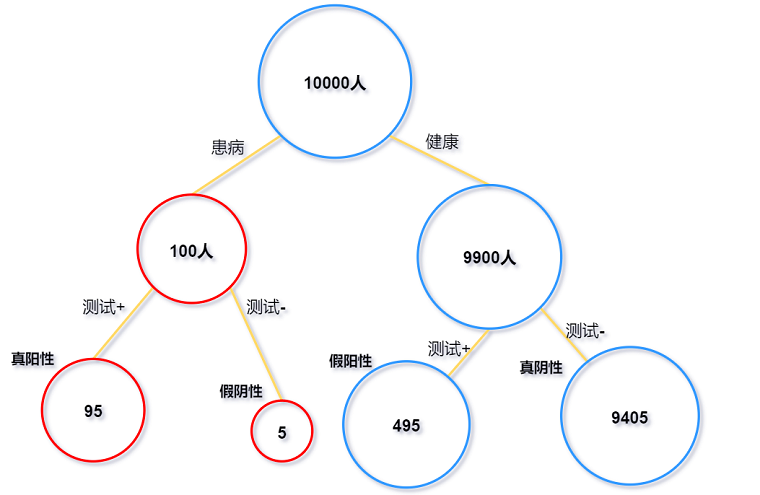
我们只关注测试结果为阳性的人, 可以看到有95人为真阳性, 以及远远超出95的495个假阳性. 所以
大多数被检测出阳性的人其实并没有患病.
2.4 条件概率也是概率
当以事件E作为条件时, 我们通过更新判断使得与该信息相一致, 从而有效地置身于已知事件E已经发生的空间.
在这个新空间下, 概率法则和以前一样都是适用的. 条件概率满足概率的所有特性! 因此, 如果用条件概率替换
无条件概率, 则前面所推导的所有有关概率的结果在以E为条件的条件概率中都适用, 特别的 :
-
条件概率在
0和1之间 -
$P(S\mid E) = 1, P(\varnothing \mid E) = 0$
-
如果$A_1, A_2, \cdots$互不相交, 则有$P(\bigcup_{i=1}^{\infty}A_i\mid E) = \sum_{i=1}^{\infty}P(A_i\mid E)$
-
$P(A^c\mid E) = 1 - P(A\mid E)$
-
容斥性 : $P(A\cup B\mid E) = P(A\mid E) + P(B\mid E) - P(A\cap B\mid E)$
2.4.1 -ω-
当我们写下$P(A\mid E)$时, 并不意味着$A\mid E$表示一个事件. 确切的说, $P(\cdot \mid E)$是一个概率函数
(function), 它基于E已经发生这一事件为事件分配概率, 而$P(\cdot)$是另一个函数, 它在不知道E是否
发生的情况下为事件分配概率. 当一个事件$A$被放入函数$P(\cdot)$时, 它会得到一个数$P(A)$; 当$A$被放入
函数$P(\cdot \mid E)$时, 会得到另一个数$P(A\mid E)$, 这个数包含事件E已经发生的信息.
条件概率也是概率的数学证明
为了从数学上证明条件概率也是概率, 确定一个正概率事件$E$, $P(E)\gt 0$, 然后对任意事件$A$, 定义$\hat{P}(A)$
$=P(A\mid E)$, 这个符号有助于强调将$P(\cdot \mid E)$看作新的概率函数. 此时只需要检验两个公理是否成立:
$\;\; \hat{P}(\varnothing \mid E) = P(\varnothing \mid E) = \frac{P(\varnothing \cap E)}{P(E)} = 0; \hat{P}(S) = P(S\mid E) = \frac{P(S\cap E)}{P(E)} = 1$.
其次, 如果$A_1, A_2, \cdots$互不相交, 则有 :
$\;\; \hat{P}(\cup_{i=1}^{\infty}A_i) = P(\cup_{i=1}^{\infty}A_i\mid E)$
$\;\;\;\; = \frac{P((A_1\cap E)\cup (A_2\cap E)\cup \cdots)}{P(E)}$
$\;\;\;\; = \sum_{i=1}^{\infty} \frac{P(A_i\cap E)}{P(E)} = \sum_{i=1}^{\infty}\hat{P}(A_i)$
所以$\hat{P}$满足概率的两条公理.
所有概率也是条件概率
相反的, 所有概率都可以看作是条件概率 : 当陈述一个概率时, 即使没有明确说明, 总有一些条件化的背景信息.
因为我们做出判断时都会隐含以往的经验. 为了确定一个看似无条件的概率$P(R)$, 实际上需要确定作为条件的
背景信息. 对这些背景信息需要仔细思考, 若结果不同就会有不同的先验概率$P(R)$.
条件概率也是概率, 并且所有概率都是有条件的.
有条件形式的贝叶斯准则和全概率公式的形式即在原公式基础上加上$\mid E$. 证明过程与证明$\hat{P}$满足
两条公理的工程类似, 也可以直接由”条件概率也是概率”这一结论得出.
例2.4.4 随机硬币续
继续例2.3.7所述问题, 假设我们现在已经看见所选取的硬抛掷3次均正面朝上, 那么接下去抛掷第4次,
仍是正面的概率是多少?
解:
设$A$事件 : 选取的硬币3次都是正面朝上, 定义一个新事件$H$代表第4次掷硬币结果为正面. 本题感兴趣
的是$P(H\mid A)$. 知道选取的硬币是否均匀可以简化计算过程. 由带有额外条件的全概率公式可知$P(H\mid A)$
等于$P(H\mid A, F)$与$P(H\mid A, F^c)$的加权和, 这两个概率因为给定了硬币信息所以很容易求 :
$\;\;\;\; P(H\mid A) = P(H\mid A, F)P(F\mid A) + P(H\mid A, F^c)P(F^c\mid A)$
$\;\;\;\; = 0.23\times 1/2 + (1-0.23)\times 3/4 \approx 0.69$
解决这个问题的另一种方法是定义一个新的概率函数$\hat{P}$, 对任意事件$B$, $\hat{P}(B) = P(B\mid A)$.
这个函数在给定$A$事件发生的条件下分配更新的概率. 由全概率公式 :
$\;\;\;\; \hat{P}(H) = \hat{P}(H\mid F)\hat{P}(F) + \hat{P}(P\mid F^c)\hat{P}(F^c)$
它与使用带有额外条件的全概率公式是一样的, 这又一次证明了条件概率也是概率的原则.
多个条件的概率函数
我们经常希望可以有不止一个条件, 以求解$P(A\mid B, C)$为例介绍几种方法 :
-
将这里的”$B$, $C$”看作是一个事件$B\cap C$, 然后应用条件概率的定义,
$\;\;\;\; P(A\mid B, C) = \frac{P(A, B, C)}{P(B, C)}$ -
运用带额外条件$C$的贝叶斯准则可以得到 :
$\;\;\;\; P(A\mid B, C) = \frac{P(B\mid A, C)P(A\mid C)}{P(B\mid C)}$ -
运用带额外条件$B$的贝叶斯准则可以得到 :
$\;\;\;\; P(A\mid B, C) = \frac{P(C\mid A, B)P(A\mid B)}{P(C\mid B)}$
2与3只是$B$, $C$的条件互换, 本书将它们分开介绍旨在强调在应用公式前应考虑什么事件扮演什么角色.
2.5 事件的独立性 independence
我们已经介绍了很多以某事件作为条件从而改变对另一事件概率判断的例子. 当事件彼此不提供任何信息时
(某事件作为条件不改变对另一事件概率判断), 称之为相互独立.
2.5.1 两个事件相互独立
称事件$A$和事件$B$是独立的, 如果 :
$\;\;\;\; P(A\cap B) = P(A)P(B)$
若$P(A)\gt 0$且$P(B)\gt 0$, 等价于
$\;\;\;\; P(A\mid B) = P(A); P(B\mid A) = P(B)$.
给定事件$B$发生不会改变$A$的概率(反之亦然 : 事件独立是相互的).
-ω- 2.5.2 独立与不相交
独立与不相交是完全不同的概率, 如果$A$和$B$不相交, 则$P(A\cap B) = 0$; 只有在$P(A)=0$或$P(B) = 0$时,
不相交的事件才会独立. 知道$A$发生就能推导出$B$一定不发生, 所以$A$提供了关于$B$的信息, 这就意味着
两个事件肯定是不独立的(除非$A$或$B$是零概率事件).
直观上说, 如果$A$不提供$B$发生或不发生的任何信息, 那么可以合理地推出$A$也不含$B^c$发生或不发生的信息.
命题 2.5.3
如果$A$和$B$相互独立, 则有$A$和$B^c$/$A^c$和$B$/$A^c$和$B^c$相互独立.
证明:
设$A$和$B$相互独立, 那么
$\;\;\;\; P(B^c\mid A) = 1 - P(B\mid A) = 1 - P(B) = P(B^c)$
或:
$\;\;\;\; P(A) = P(A\cap (B\cup B^c)) = P(A\cap B) + P(A\cap B^c) = P(A)P(B) + P(A\cap B^c)$
-->$P(A\cap B^c) = P(A)(1 - P(B)) = P(A)P(B^c)$.
所以$A$和$B^c$独立, 将$A$和$B$的角色互换, 就得到$A^c$和$B$相互独立, 利用$A$和$B^c$相互独立的结论可以
得到$A^c$和$B^c$相互独立.
我们通常还需要讨论3个或更多个事件的独立性.
定义 2.5.4 三事件独立
如果下面等式都成立, 则说明事件$A$、$B$和$C$是独立的 :
$\;\;\;\; P(A\cap B) = P(A)P(B)$
$\;\;\;\; P(A\cap C) = P(A)P(C)$
$\;\;\;\; P(B\cap C) = P(B)P(C)$
$\;\; P(A\cap B\cap C) = P(A)P(B)P(C)$
如果满足前3个条件, 则称$A$、$B$和$C$是 两两独立 的. 但两两独立并不意味着独立 : 有可能只通过事件$A$
或事件$B$不能对$C$发生提供任何信息, 但如果$A$和$B$同时发生, 这个信息可能会与$C$发生与否高度相关.
例 2.5.5 两两独立并不意味独立
考虑两枚均匀硬币, 相互独立抛掷, 设事件$A$代表第一枚硬币朝上, 事件$B$代表第二枚硬币正面朝上, 事件$C$
代表两枚硬币结果相同.
这时, $A$、$B$和$C$是两两独立的但不是相互独立的, 因为$P(A\cap B\cap C) = 1/4$, 而$P(A)P(B)P(B) = 1/8$.
关键点在于只知道$A$或$B$发生时不能提供$C$是否发生的任何信息; 但是知道$A$和$B$同时发生就可以提供给我们
关于事件$C$的信息(此时$C$一定发生). 另一方面, 有人会总结说independence means multiply, 但
$P(A\cap B\cap C) = P(A)P(B)P(C)$也不能说明就是独立; 比如一个极端例子 : $P(A) = 0$,
这时等式变成$0 = 0$,无论$B$和$C$是否独立都成立.
类似地, 可以定义任意数量的事件间的独立性. 直观来说, 就是在知道任意事件的子集发生的情况下,
无发提供关于不在该子集种的事件的任何信息.
定义 2.5.6 多事件的独立性
对于$n$个事件$A_1, A_2,\cdots , A_n$的独立性, 要求任意2个事件满足$P(A_i\cap A_j) = P(A_i)P(A_j), i\not=j$,
任意3个事件满足$P(A_i\cap A_j\cap A_j) = P(A_i)P(A_j)P(A_k), i、j、k两两不同$, 类似的, 对所有4,
5,$\cdots$均满足. 对于不可数事件, 称它们是独立的如果任意可数子集中的事件是独立的.
条件独立也用类似的方法定义.
定义 2.5.7 条件独立
事件$A$和事件$B$称作是关于事件$E$条件独立的, 如果
$\;\;\;\; P(A\cap B\mid E) = P(A\mid E)P(B\mid E)$.
-ω- 2.5.8 独立vs条件独立
如果将独立和有条件的独立混淆, 很容易造成糟糕的错误. 条件独立不能推出独立, 反之亦然. 两个事件关于
$E$条件下是条件独立的, 但关于$E^c$不存在条件独立. 下面介绍一些例子.
例 2.5.9 条件独立不意味独立
回到例2.3.7, 假设我们抽中的是一枚均匀硬币或一枚正面朝上的概率为$3/4$的不均匀硬币, 但不知道抽到的
是哪一枚. 多次投掷硬币, 如果给定选取的硬币是均匀硬币这一条件, 则硬币的投掷是独立的, 每次正面朝上的
概率是$1/2$. 类似如果给定选取的硬币是不均匀的, 则每次投掷相互独立, 每次正面朝上的概率是$3/4$.
然而, 硬币的投掷不是无条件独立的, 因为如果不知道选择的是哪一枚硬币, 那么观察到的投掷结果的序列会提供
硬币均匀与否的信息, 这将有助于预测下一次同一枚硬币的投掷结果.(也就是之前的投掷结果会提供给我们这枚
硬币的信息, 进而帮助我们预测下一次投掷的结果).
例 2.5.10 独立不意味条件独立
假设只有我的朋友Alice和Bob给我打过电话📞, 每天他俩都会给我打电话 : 令事件$A$代表Alice
给我打电话, $B$代表Bob给我打电话, 则$A$和$B$是无条件独立的. 但假设我现在听到了一声电话
铃声, 基于这一事实, $A$和$B$就不再独立了 : 如果这个电话不是Alice打的, 那就肯定是Bob打的.
换句话说, 令$R$事件代表听到电话响了, 则有$P(B\mid R) = P(B\mid A^c, R\lt 1$. 所以$B$和$A^c$在
给定$R$时不是条件独立的, 对于$A$个$B$也是如此. (基于条件$R$, $A$和$B$从无条件独立到不相关).
例 2.5.11 给定$E$条件独立vs给定$E^c$条件独立
假设有两种课程 : 好的课程和坏的课程. 在好的课上, 如果你努力, 就很有可能得A. 在坏的课上, 教授随机
分配给学生分数, 而不管他们是否努力. 令$G$事件表示这个课程是好的, $W$事件表示你学习努力, $A$事件
表示你的得分是A. 此时, 给定$G^c$, $A$和$W$是条件独立的; 但给定$G$, $A$和$W$却不是条件独立的!
2.6 贝叶斯准则的一致性
一个关于贝叶斯准则的重要性质是它是一致的 : 如果接收到多个信息并希望纳入所有的信息去更新之前的
概率, 不管按顺序更新, 即以此接受一个信息, 还是同时一次性将所有信息纳入, 结果均相同. 例如, 假设
正进行一个为期一周的试验, 在每天结束时生成数据. 我们可以每天基于当天的数据利用贝叶斯准则更新
之前的概率; 或者也可以出去度假一周, 回来时基于一周的数据一次性进行更新, 两种更新方法结果相同.
例 2.6.1 检测一种罕见疾病, 续
在例2.3.9中检测结果为阳性的Fred, 决定进行第二次检测. 新的检测结果与之前的结果相互独立, 且有
相同的真阳性率和真阴性率. 不幸的是, 第二次的结果也为阳性. 求Fred基于这些证据确认患有此病的概率,
用两种方法 : 同时考虑两次检测结果; 分步考虑两次检测结果.
解:
令$D$事件表示他确实患病, $T_1$事件表示第一次检测结果为阳性, $T2$事件表示第二次检测结果为阳性.
例2.3.9中运用了贝叶斯准则和全概率公式求$P(D\mid T_1)$. 另一种更快速的方法是通过贝叶斯准则
的几率形式,
$\;\;\;\; \frac{P(D\mid T_1)}{P(D^c\mid T_1)} = \frac{P(T_1\mid D)P(D)}{P(T_1\mid D^c)P(D^c)} = \frac{1}{99}\times \frac{0.95}{0.05}\approx 0.19$
$\;\;\;\; P(D\mid T_1) = odds/(1 + oddds) = 0.19 / (1 + 0.19)\approx 0.16$.
用几率形式计算更快的原因是不需要计算普通贝叶斯准则的分母 : 无条件概率$P(T_1)$. 现在依旧用几率
形式计算第二次检测结果也为阳性会怎样.
一步法 (One-step method) : 将两个检测结果一次性都考虑在内进行概率更新,
$\;\;\;\; \frac{P(D\mid T_1,T_2)}{P(D^c\mid T_1,T_2)} = \frac{P(D)P(T1,T2\mid D)}{P(D^c)P(T1,T2\mid D^c)}
= \frac{1}{99}\times\frac{0.95^2}{0.05^2}\approx 3.464$
对应着$0.78$的概率.
两步法(Two-step method) : 在完成第一次检测后, 由上面结果可知Fred患有此病的后验几率为 :
$\;\;\;\; \frac{D\mid T_1}{P(D^c\mid T_1)} = \frac{1}{99}\times \frac{0.95}{0.05}\approx 0.19$
这些后验几率成为新的先验几率, 然后基于第二次检测结果将概率更新为
$\frac{P(D\mid T_1,T_2)}{P(D^c\mid T_1,T_2)} = \frac{P(D\mid T_1)P(T_2\mid D,T_1)}{P(D^c\mid T_1)P(T_2\mid D^c,T_1)} = \frac{P(D\mid T_1)P(T_2\mid D)}{P(D^c\mid T_1)P(T_2\mid D^c)} = (\frac{1}{99}\times \frac{0.95}{0.05})\times \frac{0.95}{0.05}\approx 3.464$
这和一步法的结果一样.
有了第二次检测结果后, 使得Fred患有此病的概率一下子从0.16跃升到0.78.
2.7 条件概率作为解决问题的工具
条件概率是解决问题的一个强有力的工具, 因为它使得我们可以按照认定的条件进行思考 : 在遇到一个问题时,
可能知道事件$E$是否发生会更容易进行求解, 那么我们可以先按$E$为条件, 在以$E^c$为条件, 分别考虑概率,
再用全概率公式求和.
2.7.1 策略 基于想知道的条件 wishful thingking
例 2.7.1 蒙提$\cdot$霍尔问题
假设在蒙提$\cdot$霍尔(Monty Hall)主持的一档电视节目Let's Make a Deal中, 一位选手从三扇门中选一扇,
其中有两扇门后面是一只山羊(后面简称山羊门), 一扇门后面是一辆车(后面简称汽车门).
Monty知道🚗在那扇门后, 然后打开剩下(不打开选手开始选择的)两扇门中的一扇. 他打开的门后面永远是山羊
(他从不暴露车的位置). 如果剩下两扇门都可以选的话(都是山羊门), 他会等可能地随机选取一扇门. 然后Monty
会让选手选择 : 是换一扇没打开的门还是不换. 如果选手的目标是得到车, 她应该换吗?
解 :
先将三扇门从$1$到$3$编号(label). 不失一般性, 可以假设选手选择的是$1$号门(如果她没有选$1$号门, 由于
对称性可以重新编号, 再利用新的排列解答). Monty打开一扇门, 出现了羊. 当选手决定要不要换一扇还没有开
的门时, 她希望可以知道什么?(condition on "wishful thinking")当然, 如果她知道车在哪里问题就简单多了,
这暗示我们可以将车的位置作为条件. 设事件$C_i$表示车在第$i$个门后面, $i = 1,2,3$. 设事件$G$为选手
每次换门且得到车, 由全概率公式 :
$\;\; P(G) = P(G\mid C_1)P(C_1) + P(G\mid C_2)P(C_2) + P(G\mid C_3)P(C_3) = $
$P(G\mid C_1)\times 1/3 + P(G\mid C_2)\times 1/3 + P(G\mid C_1)\times 1/3$.
假设选手换门, 如果车在$1$号门, 则换门就输了, 所以$P(G\mid C_1) = 0$. 如果车在$2$/$3$号门后面, 因为
Monty肯定选择山羊, 剩下的没有打开的门一定是汽车门, 这时换门就能得到车, 所以有 :
$\;\;\;\; P(G) = 0\times 1/3 + 1\times 1/3 + 1\times 1/3 = \frac{2}{3}$.
所以换门会有$2/3$可能性得到车, 应该换.
下图给出上述讨论的树状图 :
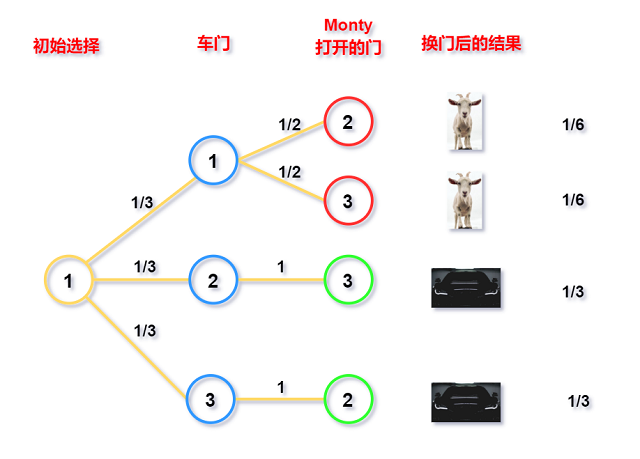
一个有趣的地方 : 当选手选择换门时, 她已经知道了Monty打开的是哪扇门; 但即使给定Monty打开门的编号,
赢得车的条件概率也为$2/3$.
$\;\;$令事件$M_j$代表Monty打开第$j(j = 2,3)$号门, 事件$G$代表得到车, 那么
$\;\;\;\; P(G) = P(G\mid M_2)P(M_2) + P(G\mid M_3)P(M_3)$.
由对称性, $P(M_2) = P(M_3) = 1/2$. 所以$P(G\mid M_2) = P(G\mid M_3) = 2/3$. 在练习题中会讨论Monty
相比于$2$号门更喜欢$3$号门的情况.
给定条件, 贝叶斯准则也适用于计算适用换门策略时成功的条件概率. 假设Monty打开了$2$号门.
(仍然设开始选择门的编号是$1$, 计算汽车也在$1$号门后且选择换门策略的概率, 也就是失败的概率)
$\;\;\;\; P(C_1\mid M_2) = \frac{P(M_2\mid C_1)P(C_1)}{P(M_2)} = \frac{(1/2)\times (1/3)}{1/2} = 1/3$.
所以给定Monty打开$2$号门这一条件, 选手一开始选择正确的概率是$1/3$, 也就意味着换门会赢得车的概率为$2/3$.
许多人刚开始接触这个问题时都觉得换门并没有什么帮助, “还剩两扇门, 其中一个有车, 所以可能性是$50$比$50$”.
在介绍完最后一章后, 我们可以发现出现这一问题是因为错误地使用了朴素概率定义.
(Monty打开$2$号门后有两条信息, 1. $2$号门后面是🐏; 2. Monty打开的是$2$号门. 我的理解是要注意Monty
打开门的概率并不是均等的, 有时是确定的, 有时是等可能的, 所以不能直接用朴素概率定义).
try simple and extreme cases
为构建正确直觉, 现在考虑一个极端例子. 假设共有$100$万扇门, 其中$10^6-1$扇门后都是山羊, 只有$1$扇门后面
是汽车. 在选手此一次选择完后, Monty打开了$10^6-2$后面都是羊的门, 让选手是否换成另一扇还没打开的门.
这时会容易察觉我们不换而成功的概率取决于第一次选择是否正确, Monty打开了$10^6-2$扇门这一条件无法被
忽略, 所以不是简单的$50$比$50$.
就像前面在例2.2.6中关于如何遇到随机女孩的假设一样, 这里换门有$2/3$胜率也是基于有关Monty
如何选择开门的假设.
2.7.2 策略: 考虑第一步
在有递归结构的问题中, 基于第一步的条件概率可以简化问题, 我们称这个策略为 一步分析(first-step analysis).
例 2.7.2 分支过程
池塘里有一只宝可梦Bobo, 1 min后, Bobo会有3种结果: 死去、分裂成两个或保持原状, 3种情况概率
相同.且此后分裂出的Bobo都将继续以这种方式相互独立下去.
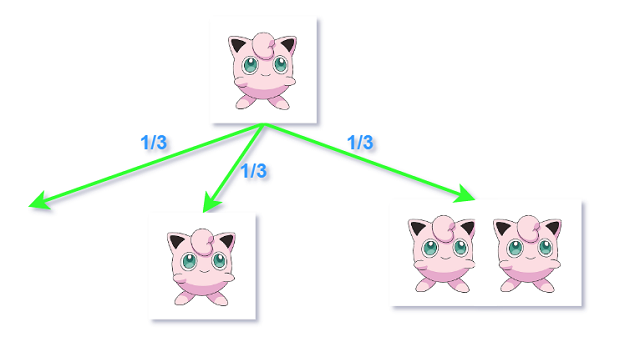
那么这个宝可梦种族最终灭亡的概率是多少?
解:
令事件$D$表示最终物种灭绝; 本题希望求$P(D)$. 令事件$B_i(i=0,1,2)$表示在1 min后由Bobo变成变形虫
的个数. 有 : $P(D\mid B_0) = 1, P(D\mid B_1) = P(D)$(如果个数保持不变, 事件也保持不变); 如果Bobo
分裂成两个, 此时原始问题就变成两个相互独立的问题 : $P(D\mid B_2) = P(D)^2$. 现在我们已经考虑了所有
可能, 利用全概率公式 :
$\;\;\;\;P(D) = P(D\mid B_0)\times \frac{1}{3} + P(D\mid B_1)\times \frac{1}{3} + P(D\mid B_2)\times \frac{1}{3}$
$\;\;\;\;\;\; = 1\times \frac{1}{3} + P(D) + P(D)^2$, 求解一元二次方程, 得到$P(D) = 1$. 所以这个物种一定会灭绝.
一步分析策略在这里是适用的, 因为这个问题在本质上是自相似的(递归) : 当Bobo保持不变或分裂成两个时,
都只是原始问题保持不变或者两个独立原始问题而已.
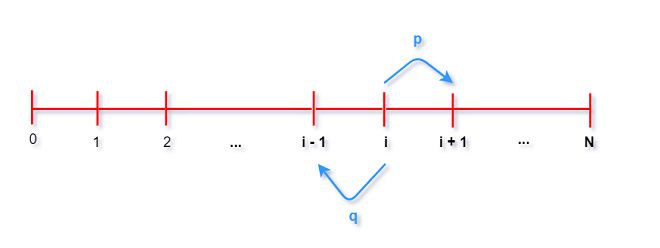
例 2.7.3 赌徒输光问题 gambler’s ruin problem
有两个赌徒A和B, 进行一系列的一美元的赌注, 赌徒A赢的概率为$p$, 赌徒B赢的概率是$q = 1 - p$.
赌徒A的初始资金为$i$美元, 赌徒B的初始资金是N - i美元, 两人资金总和始终为$N$.
可以将这个问题看作是$0$至$N$之间的随机游走(random walk), 设想一个人开始站在位置$i$, 向右走一步的
概率是$p$, 向左走一步的概率是$q = 1 - p$. 当走到了$0$或$N$的位置, 即A破产或B破产, 游戏结束.
那么A赢得比赛的概率是多少? 这个游戏会永远持续下去吗?
解:
可以看出该问题和Bobo繁殖过程一样, 存在一个递归结构 : 在第一步后, 问题又变成了一模一样的问题,
除了A的资金变为$i-1$或$i+1$(same problem with different initial condition). 令事件$p_i$表示
A的初始资金为$i$时最终赢得比赛的概率. 这里用到一步分析法. 令$W$为事件表示A最终赢得比赛.
由全概率公式, 基于第一步的结果可以得到 :
$\;\;\;\;p_i = P(W\mid A的初始资金为i,第一轮赢)\times p + P(W\mid A的初始资金为i,第一轮输)\times q$
$\;\;\;\;\;\;= P(W\mid A的初始资金为i+1)\times p + P(W\mid A的初始资金为i-1)\times q$
$\;\;\;\;\;\;= p_{i+1}\times p + p_{i-1}\times q$.
上式对于$1$到$N-1$的所有$i$都成立, 边界条件 : $p_0 = 0, p_N = 1$. 现在为求解$p_i$需要用到差分方程.
$\cdots$(省略差分计算过程) A以初始资金$i$赢得游戏的概率为 :
$\;\;\;\;p_i = \frac{i}{N}$.
由对称性可知, B以初始资金$N - i$赢得游戏的概率可以通过转换$p$和$q$, 以及$i$和$N - i$得到. 可以
证明对所有的$i$和所有的$p$, 有$P(A赢) + P(B赢) = 1$, 所以游戏必定会结束 : 永不结束(无人赢得比赛)
的概率为$0$.
最后我们来看一下A每轮赢得游戏的概率为$0.49$, 初始资金相等时A能赢得游戏的概率 :
| 初始资金 | 赢得游戏概率 |
|---|---|
| $20$ | $0.40$ |
| $100$ | $0.12$ |
| $200$ | $0.02$ |
即使游戏有一点不公平, 只要玩的轮次够多, 总有有一点会输光. 这也就是例子叫做gambler's ruin problem
的原因.
2.8 陷阱与悖论
接下来的2个例子是在法律背景下出现的条件性思维谬误. 检察官的错误是混淆了$P(A\mid B)$和$P(B\mid A)$;
辩护律师的错误则在于没有将所有的证据作为条件.
-ω- 2.8.1 控方证人的错误
1998年, Sally Clark由于她的两个孩子在出生不久便死亡, 因而被指控谋杀幼童. 在审讯期间, 控方的一个
专家证人证实新生儿死于婴儿猝死综合征(Sudden Infant Death Syndrome, SIDS)的概率为$1/8500$, 所以
两个新生儿由于婴儿猝死综合征SIDS死亡的概率为$(1/8500)^2$, 大约为$7300$万分之一. 因此他认为Clark
是清白的概率仅为$7300$万分之一.
这个推理至少有2个问题. 首先专家证人求出两个孩子死于SIDS的概率直接是两个事件的概率相乘; 我们知道,
只有当一个家庭成员之间死于SIDS是相互独立时才能这么做. 如果遗传因素或家庭特有的风险因素导致
某些家庭内的所有新生儿面临SIDS的风险增加, 这种独立性就不再成立了.
其次, 这个所谓的专家将两个不同的条件概率混淆了 :
$P(清白\mid 证据)和P(证据\mid 清白)$是不一样的. 专家声称: 如果在被告人是在清白的情况下, 两个孩子死亡
的概率很低, 即$P(证据\mid 清白)$很小. 但人们真正关注的是, 给定现在所有证据(两个孩子均死亡)条件下, 报
告人仍清白的概率, 即$P(清白\mid 证据)$.(我们不能提前假设被告人有罪/无罪). 由贝叶斯准则 :
$\;\;\;\; P(清白\mid 证据) = \frac{P(证据\mid 清白)P(清白)}{P(证据)}$,
所以为了计算$P(清白\mid 证据)$, 这里需要考虑$P(清白)$, 也就是被告清白的先验概率. 这个概率是很高的 :
一个母亲蓄意杀害两个婴儿是极其罕见的! 基于现有证据的后验概率是对很低的$P(证据\mid 清白)$和很高
的$P(清白)$的一种平衡. 专家的结果$(1/8500)^2$是有问题的, 它只是整个计算式中的一部分.
-ω- 2.8.2 辩护律师的错误
一个女人被谋杀了, 她的丈夫因有谋杀嫌疑而被审问. 证据显示被告人有家暴史. 辩护律师认为, 家暴的证据
应该由于与罪行不相干而排除在外, 因为在10000个虐待妻子的男子中只有一个后来会谋杀妻子. 法官是否
应该接受辩护律师的提议, 将这项证据排除在外?
假设辩护律师的$1/10000$是准确的, 进一步假设以下事实: 10个男子中有1个会对他的妻子施暴, 5个
被谋杀的已婚妇女中有1个是被丈夫杀害的, 杀害妻子的丈夫中有$50\%$曾对妻子实施家暴.
令$A$事件表示丈夫对妻子施暴, $G$事件表示丈夫有罪, 则辩护律师的论点为$P(G\mid A) = 1/1000$, 因此
即使基于以前有家暴史, 丈夫有罪的概率也很低.
然而, 辩护律师没有以一个关键事实为条件: 在这个案子中, 我们已知妻子被杀害了. 因此, 相关的概率不是
$P(G\mid A)$, 而是$P(G\mid A, M)$, 其中$M$事件表示妻子被谋杀.
$\;\;\;\;$由给定额外条件的贝叶斯准则, 得 :
$\;\;\;\; P(G\mid A, M) = \frac{P(A\mid G, M)P(G\mid M)}{P(A\mid M)}$
$\;\;\;\;\;\; = \frac{P(A\mid G, M)P(G\mid M)}{P(A\mid M, G)P(G\mid M) + P(A\mid M, G^c)P(G^c\mid M)}$
$\;\;\;\;\;\; = \frac{0.5\times 0.2}{0.5\times 0.2 + 0.1\times 0.8} = \frac{5}{9}$
家暴的证据将有罪的概率从$20\%$提高到了$50\%$以上, 所以被告人有家暴史给出了关于他有罪的概率的关键
信息, 反驳了辩护律师的观点.
注意到上述计算中根本没有用到$P(G\mid A)$, 它与我们的计算无关, 因为其没有考虑妻子被谋杀的事实. 我们必须
基于所有证据进行计算.
接下来以一个条件概率和数据聚合的悖论结束本章.
例 2.8.3 辛普森悖论 Simpson Paradox
有两个医生, Hibbert和Nick每个人都能执行两种手术: 心脏手术和创可贴移除手术.
两个医生执行100次手术的相应记录见下表 :
如果我们要去看医生的话, 应该大多会选择Hibbert医生 : Hibbert医生在心脏手术方面比Nick医生
的成功率高 : $70/90\approx 78\%$的成功率对$2/10 = 20\%$的成功率; Hibbert医生在创口贴移除
手术方面也比Nick医生的成功率高 : $10/10 = 100\%$的成功率对$81/90 = 90\%$的成功率. 但是如果
将两种手术的数据合并, Hibbert医生100次手术有80次成功, 但Nick医生100次手术有83次
成功: Nick医生的手术成功率比Hibbert医生的还要高!
用白点表示成功的手术, 灰点表示失败的手术:
事实上, 据推测, 因为Hibbert医生是高级医师, 所以会执行更多的心脏手术, 这本质上比创口贴移除手术
风险高很多. 整体手术成功率比较低并不是由于在任何类型的手术中技巧欠佳, 而是他大部分手术风险比较高.
下面用符号来详细解释. 对于事件$A、B和C$, 我们说出现了辛普森悖论, 如果有,
$\;\;\;\;\;\;P(A\mid B, C)\lt P(A\mid B^c, C)$
$\;\;\;\;\;\;P(A\mid B, C^c)\lt P(A\mid B^c, C^c)$
但是$\;\;\;\;\;\;P(A\mid B)\gt P(A\mid B^c)$
在本例中, $A$事件表示手术成功, 事件$B$为Nick医生执行手术($B^c$:Hibbert医生执行手术), 事件$C$
为手术是心脏手术.
这一现象可以用全概率公式以数学形式解释 :
$\;\;\;\;P(A\mid B) = P(A\mid B, C)P(C\mid B) + P(A\mid B, C^c)P(C^c\mid B)$
$\;\;\;\;P(A\mid B^c) = P(A\mid B^c, C)P(C\mid B^c) + P(A\mid B^c, C^c)P(C^c\mid B^c)$
虽然已知
$\;\;\;\;P(A\mid B, C)\lt P(A\mid B^c, C)$
和
$\;\;\;\;P(A\mid B, C^c)\lt P(A\mid B^c, C^c)$
但权重$P(C\mid \cdot)$和$P(C^c\mid \cdot)$会改变整体和的结果. 在我们看来
$\;\;\;\;\;\;P(C^c\mid B) > P(C^c\mid B^c)$. 因为Nick医生更多执行风险低的创口贴手术, 且这个差别
足够大, 使得$P(A\mid B)\lt P(A\mid B^c)$.
将不同类型的手术数据合并会造成对医生能力的误读, 这是因为没有考虑不同医生倾向于执行的手术类型也不同.
当我们在考虑类似于手术类型这种混杂的变量时, 应该用分类的数据去了解真实情况.
辛普森悖论在现实生活中经常出现, 请在下面例子中找出造成悖论的事件$A$、$B$和$C$.
-
Ac成功率 :
Y某在简单题和困难提的Ac率(Ac题/所有题)都比代某高, 但所有题目的Ac率反而是
代某略高一筹. 实际上是因为代某只刷简单题. -
大学生招生中的性别歧视: 在
19世纪70年代, 美国加州大学伯克利分校研究生的录取比例中男性明显
比女性有优势, 因此收到了关于性别歧视的指控. 然而在个别学院, 女士的录取率比男生高. 实际上是因为
女士更倾向于申请竞争激烈的学院而男生更倾向于申请竞争压力小的学院. -
吸烟对健康的影响:
Cochran发现在任意年龄组中吸香烟的死亡率都会超过吸雪茄的死亡率, 但是因为
吸香烟的人总体比吸雪茄的人年轻, 因此造成整体的吸香烟的死亡率比吸雪茄的低.
2.9 要点重述
给定条件$B$时, $A$的条件概率为
$\;\;\;\;\;\;P(A\mid B) = \frac{P(A\cap B)}{P(B)}$
条件概率具有与概率完全相同的属性, 但是$P(\cdot \mid B)$更新了我们对事件的不确定性, 从而反映出
观察到的证据$B$. 在观察证据$B$之后概率保持不变的事件称为独立于$B$. 当给定第三个条件$E$时, 两个
事件也可以是条件独立的. 条件独立不能推出非条件独立, 反之亦然.
贝叶斯准则和全概率公式是两个条件概率的重要结论. 贝叶斯准则将$P(A\mid B)$和$P(B\mid A)$相关联,
全概率公式通过分割样本空间并计算划分的每个部分的条件概率从而得到无条件概率.
条件思维对于解决问题非常有帮助, 因为它允许我们将问题分解成更小的部分, 分别考虑所有可能的情况,
然后将它们重新组合. 在使用该策略时, 首先应该尝试将一些信息作为条件, 这些信息的特征是如果知道
后就会使问题简单化, 也就是将希望知道的信息(wishful thinking)作为条件. 当一个问题涉及多个
阶段时, 将第一步作为条件获得递归关系是有帮助的.
条件思维常见错误包括:
-
将先验概率$P(A)$和后验概率$P(A\mid B)$混淆.
-
检察官谬误, 将$P(A\mid B)$和$P(B\mid A)$混淆.
-
辩护律师错误, 没有将所有证据条件化
-
没有意识到辛普森悖论以及忽略仔细思考是否应该合并数据的重要性.
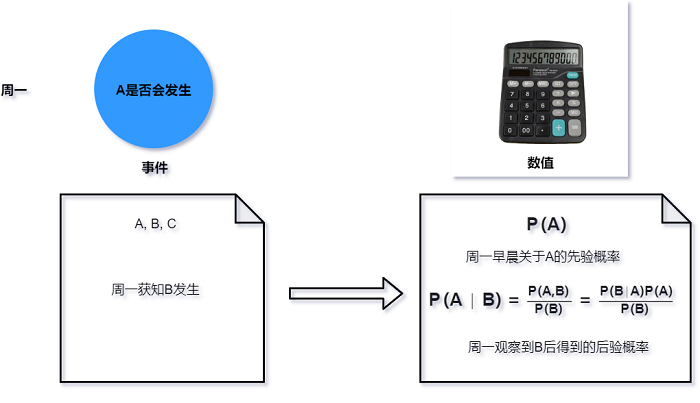
下图说明了当新证据按顺序出现后, 概率如何更新. 假设我们对事件$A$感兴趣, 在周一早上, 事件$A$的
先验概率为$P(A)$. 如果在周一下午观察到了事件$B$的发生, 这时可以利用贝叶斯准则(或条件概率定义)
计算后验概率$P(A\mid B)$.
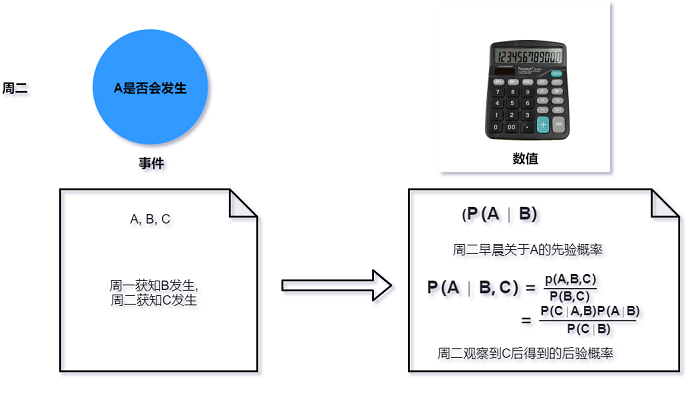
在周二早上我们可以把上述求得的后验概率当作新的先验概率, 然后继续收集证据. 假设在周二观察到
新证据$C, 这时就可以用不同方法计算新的后验概率P(A\mid B, C). 如果还需要收集新证据, 这个
概率就可以被看作新的先验概率.
👍🏻