本笔记内容来源于算法基础课

高斯消元

给定包含$m$个方程和$n$个未知数的线性方程

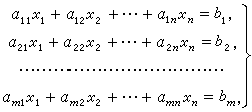
高斯消元法在时间复杂度为$O(n^3)$进行求解

解的情况:

1. 无解
2. 无穷多组解
3. 唯一解

将等式两边的常数提取构成的系数矩阵大小为$n \times (n+1)$

高斯消元的涉及的操作有(初等行列变换)：

1. 将某一行乘一个非零的数
2. 交换某两行
3. 把某行的若干倍加到另一行上去

通过以上操作可以将系数矩阵转化为一个上三角矩阵

对于上三角矩阵，最后一行只包含一个未知数可以求出，而上一行会比下一行多出一个未知数，因此可以不断向上求出。

得到的上三角矩阵的情况有：

1. 完美阶梯行：有唯一解
2. 不完美阶梯行
   • 0 = 非零：无解
   • 0 = 0：无穷多组解

高斯消元算法思路：

1. 枚举对于每一列c：
2. 找到系数绝对值最大的一行（未进行固定）
3. 将该行固定到最上面（所有未固定行之中）
4. 将该行第一个数变成1
5. 将该行的下面所有行的第c列消成0
6. 倒着求解每个未知数

int n;
double[][] a; // n * (n+1) 系数矩阵, c in [0, n], r in [0, n)
double eps = 1e-6;
int gauss() { // 0 唯一解 1 无解 2 无穷多组解
    int r = 0; // 未固定的起始行r
    for (int c = 0; c < n; c++) { // 枚举所有系数每一列c
        int t = r; // 绝对值最大行t
        for (int i = r; i < n; i++) 
            if (Math.abs(a[i][c]) > Math.abs(a[t][c]))
                t = i;

        if (Math.abs(a[t][c]) < eps) continue; // 为0跳过

        for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]); // 交换两行
        for (int i = n; i >= c; i--) a[r][i] /= a[r][c]; // 系数变为1，注意需要逆序更新（或存储第一个系数）
        for (int i = r + 1; i < n; i++) // 枚举后面的每一行
            if (Math.abs(a[i][c]) > eps) 
                for (int j = n; j >= c; j--) // [c, n]
                    a[i][j] -= a[r][j] * a[i][c]; // 每一个数减非固定行的数乘以当前行的第一个数

        r++; // 完成固定一行
    }

    if (r < n) {
        for (int i = r; i < n; i++) 
            if (Math.abs(a[i][n]) > eps) // 最右边系数存在非零
                return 2;
        return 1;
    } else {
        for (int i = n - 1; i >= 0; i--) 
            for (int j = i + 1; j < n; j++) // 将该行的最右系数减去 下面的所有元素(变量)乘以下面的最右系数
                a[i][n] -= a[i][j] * a[j][n];
        return 0;
    }   
}