目录传送门

3.2 定点数补码加、减法运算器的设计

一、四位串行加法器的设计（基于一位全加器FA）

加法器：

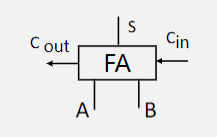
输入端：
$A$和$B$：分别表示加数和被加数
$C_{in}$：相邻低位向本位的进位输入位

输出端：
$C_{out}$：本位向相邻高位的进位输出位
$S$：本位和

四位串行加法器：

将四个加法器，按照从低位到高位的次序，依次将低位的进位输出位连接到高位的进位输入位；

如图：

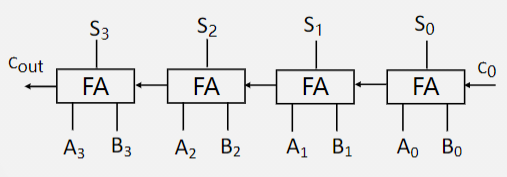
当Ai、Bi给定时，最低位的进位输入为0，就可以进行两个四位二进制加法运算了；

二、四位串行加/减法器的设计

设计思路： $[X - Y]_补 = [X]_补 - [Y]_补 = [X]_补 + [-Y]_补 $
(将减法运算转化为加法运算 )

在之前的基础上做出改进可得加减法运算器：

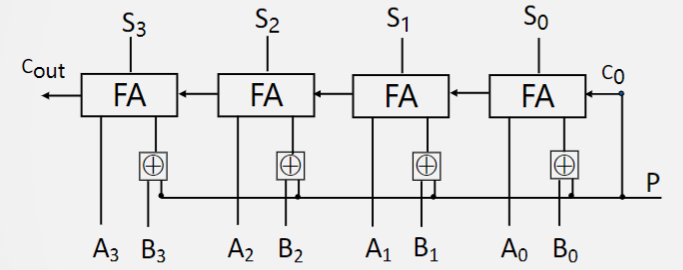
当 $p = 0$ 时，$Y$值不变，根据公式$[ X + Y ]_补 = [ X ]_补 + [ Y ]_补$，实现加法运算。

当$ P=1$时，$B$相当于取反加一（异或相当于取反，最低位进位$C0$为$1$表示加一），变为了$[-B]_补$。 根据公式$[ X ] 补 − [ Y ] 补 = [ X ] 补 + [ − Y ] 补 $，实现减法运算。

三、带溢出检测功能的加/减法运算器

上一节 学到了检测溢出的三种硬件实现方法，这次给出其对应的实现电路；

方法一：

已知$V = X_0Y_0\overline{S_0} + \overline{X_0Y_0}S_0 $（设$X_0，Y_0$为参加运算数的符号位，$S0$为结果的符号位）

则电路实现如下图：

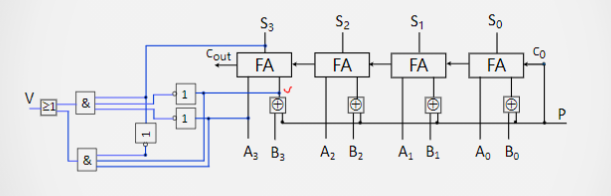
公式中，$X_0$的值就是$A_3$的值，$Y_0$的值就是$B_3$的值，而$S_0$的值则是$S_3$的值

方法二：

已知$ V= C0 \bigoplus C1$ (1表示溢出，0表示每溢出)

则对应的检测电路如图示：

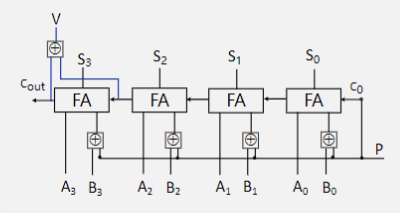
将向最高位的进位输入和最高位的进位输出异或起来就行；

方法三：

使用变形补码，直接将两个符号位做异或运算，值为1则溢出，反之没有溢出（过于简单，不上图了）

四、无符号数溢出检测功能的加减运算器

对于无符号加法溢出检测，只要看最高位有无进位即可；

对于无符号减法溢出检测，最高位一定会出现进位，如果没出现进位则表示溢出；

因此，可对最高位进位做取反，如果结果为1则有溢出，反之则没有溢出；

如图在加法器的基础上添加一个二路选择器即可检测溢出：

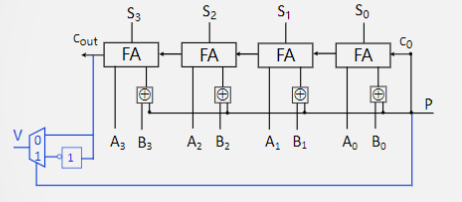
$P$作为二路选择器的输入端；
当$p = 0$时，将最高位进位作为输出结果；(检测加法溢出)
当$p = 1$时，将最高位进位取反作为输出结果；(检测减法溢出)

五、串行进位

之前讲的加法器都是低位输出作为高位的输入，以此类推, 串行的方式进位的；

分析每一个$C_i$的进位表达式可得：

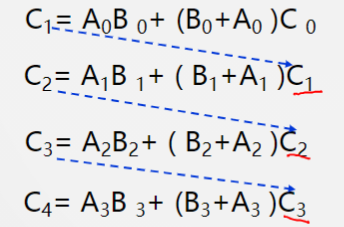
（$C_{out} = A_iB_i + （B_i + A_i）C_{in}$）

四个进位之间形成了串行连接关系，对于每一个$C_i$都得等待$C_{i-1}$计算出来，以此类推；
随着运算器位数的增加，串行进位会导致较大的时延，速度比较慢；

为了消除串行的时延，必须在逻辑表达式式子上打破递推关系。
将每一项代入后面一项，依此类推，这样得到的进位就只和$A_i$、$B_i$和$C_0$有关系了，不再有相互依存的等待关系。

对于$C_4$，我们又能拆解出两个表达式（C4的两个部分）：

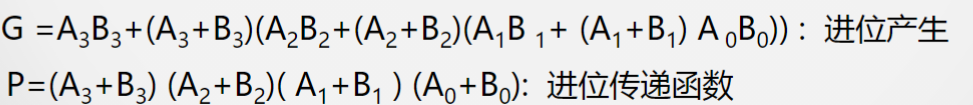
（$C_4 = G + P C_0$）

$G$ 描述了$A_i$和$B_i$对进位的影响；
$P$ 描述了$C_0$对进位的影响；

得到了逻辑表达式，就可以设计并行电路对串行做改进。

六、多位串行进位与并行进位运算器

通过对四位串行进位加法器的并行改造和封装，我们得到了四位具有并行进位功能的ALU：

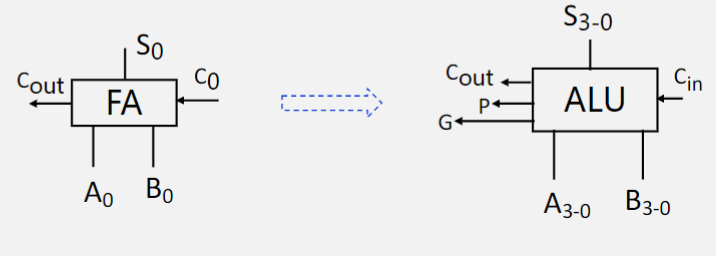
其中$C_{out} = G + PG_0$

如何用四位并行ALU去构造位数更多的ALU呢？

最简单的方法是将更多的ALU串行链接：

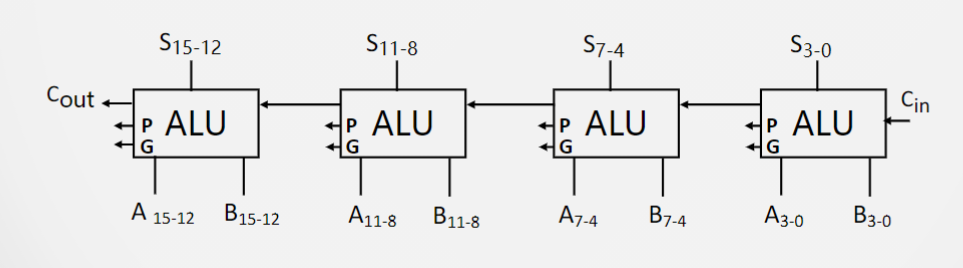
该运算器分为四段（每段四位），每段内部是并行进位，每段之间是串行进位。

仿照对四位加法器的改造方法对该串行ALU进行改造，这样可以得到十六位的完全并行ALU：

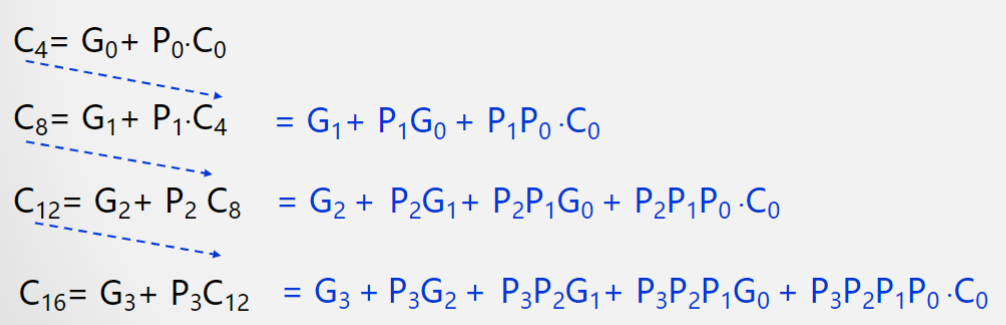
利用代入的方法消除串行进位之间的串行关系，我们可以重新用推得的逻辑表达式改造电路来产生每个ALU需要的进位输入；

改造封装之后如图，并行进位部件可以并行处理各ALU的输出：

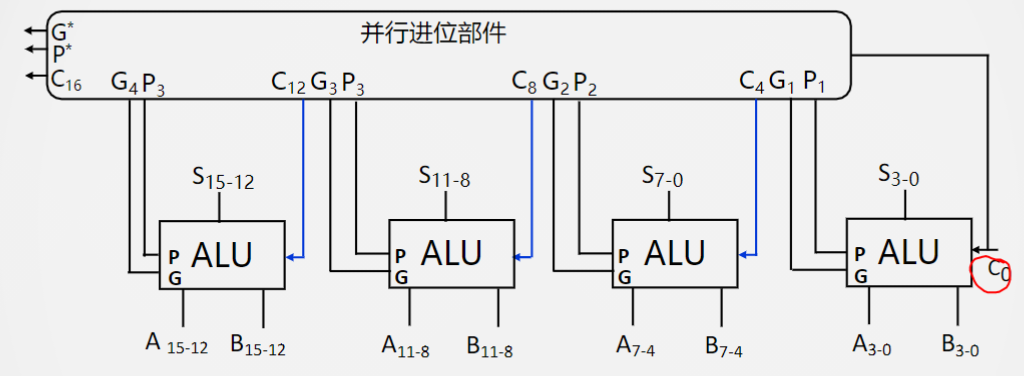
不要忘记最开始的最低位进位输入$C_0$和最高位并行范围更大的输出$P$和$G$