树的基本概念、二叉树、树和森林
树的基本概念
-
树是由根节点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点,所定义的关系称为父子关系。父子关系在树的节点之间建立了一个层次结构。在这种层次结构中有一个节点具有特殊的地位,这个节点称为该树的根节点,或称为树根。
-
空集合也是树,称为空树。空树中没有节点;
-
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
-
节点的度:一个节点含有的子节点的个数称为该节点的度;
-
叶节点或终端节点:度为0的节点称为叶节点;
-
非终端节点或分支节点:度不为0的节点;
-
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
-
兄弟节点:具有相同父节点的节点互称为兄弟节点;
-
树的度:一棵树中,最大的节点的度称为树的度;
-
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
-
树的高度或深度:树中节点的最大层次;
-
节点的祖先:从根到该节点所经分支上的所有节点;(包括该节点的父结点!)
-
子孙:以某节点为根的子树中任一节点都称为该节点的子孙;
-
森林:由若干棵互不相交的树的集合称为森林。
(PS:空树构成的集合也是森林,不过不考,了解一下)
-
性质:树的结点数比边数多1.
二叉树
(1) 二叉树的定义及其主要特征
a. 二叉树的基本形态:空二叉树、单节点二叉树、左子树、右子树
b. 性质:
[1] 在非空二叉树中,第 i 层上至多有2^( i - 1) 个结点。
[2] 深度为 k 的二叉树至多有2^k - 1个 结点 (由上面的结论推的)
[3] 对任何一棵二叉树,若其叶子结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。(比较重要)
[4] n个结点的完全二叉树深度为:log2(n)向下取整 + 1
[5] 二叉树的堆式存储: 节点p的左儿子:2x,右儿子:2x+1
(还可以求出p的父结点:p / 2 向下取整)
c. 两种特殊的二叉树
[1] 满二叉树:一颗深度为k且有2^k-1个结点的二叉树
[2] 如果深度为k,有n个结点的二叉树,当且仅当其每个结点都与深度为k的满二叉树中编号从1到n的结点一一对应,该二叉树称为完全二叉树
(2) 二叉树的顺序存储结构和链式存储结构
(3) 二叉树的遍历
a. 前序遍历
b. 中序遍历
c. 后序遍历
d. 根据前序 + 中序重建二叉树(☆ AcWing 18)
(4) 线索二叉树的基本概念和构造
对二叉树节点的指针域做如下规定:
a. 若节点有左孩子,则Lchild指向左孩子,否则指向直接前驱;右孩子同理;
b. 增加两个标志域,Ltag表示指向的是子节点还是前驱;Rtag同理
c. 指向前驱和后继的指针叫做线索。按照某种次序遍历,加上线索的二叉树称之为线索二叉树
树、森林
(1) 树的存储结构
a. 只存父节点
b. 邻接表存储所有子节点
c. 左儿子右兄弟
(2) 森林F与二叉树T的转换
a. 森林(树)中叶子节点数 = 转换后的二叉树中有右儿子的节点数 + 1
(读者可以画一个森林转化成二叉树验证)
b. F的前序遍历就是T的前序遍历
c. F的后序遍历就是T的中序遍历
(3) 树和森林的遍历
a. 前序遍历
b. 后序遍历
(没有中序遍历的原因:不存在中间的结点,也就是有多个儿子结点)
考题:
-
对于以上知识,重点的有:
-
结点的计算
- 前序+中序 —> 二叉树(Acwing18)
-
森林、树和二叉树的互相转化
-
2011-4、2011-5、2011-6、2012-3、2013-5、2014-4、2014-5、2014-41、2015-2、2016-5、2016-42、2017-4、2017-5、2018-4、2019-2、2020-3、2020-4
-
对于题目给定的前序和后序序列,求不会是中序序列的:我们可以把前序和每个给定的中序来构造出
二叉树,再看其后序序列是不是题目给定的。从而判断出答案。
-
由前序和后序序列能唯一构造二叉树的条件:当且仅当这棵树中只有度为0和2的结点,就可以唯一确定出二叉树。
-
- 结论:包含n个结点的二叉树的数量就是第n个卡特兰数:Cn =C(2n,n)/(n+1) (背过)
(另外一个应用: 给定一个序列,通过一个栈将这个序列排序,得到的不同序列的数量也是卡特兰数!!)
-
一个森林有n个结点,那么它的边数是n-1:如果题目给定了点数和边数问有几个树,我们就可以用n-1条边减掉给定的边数就得到多的树,再加上原来的一个就得到所有的树量。
-
正则后k树
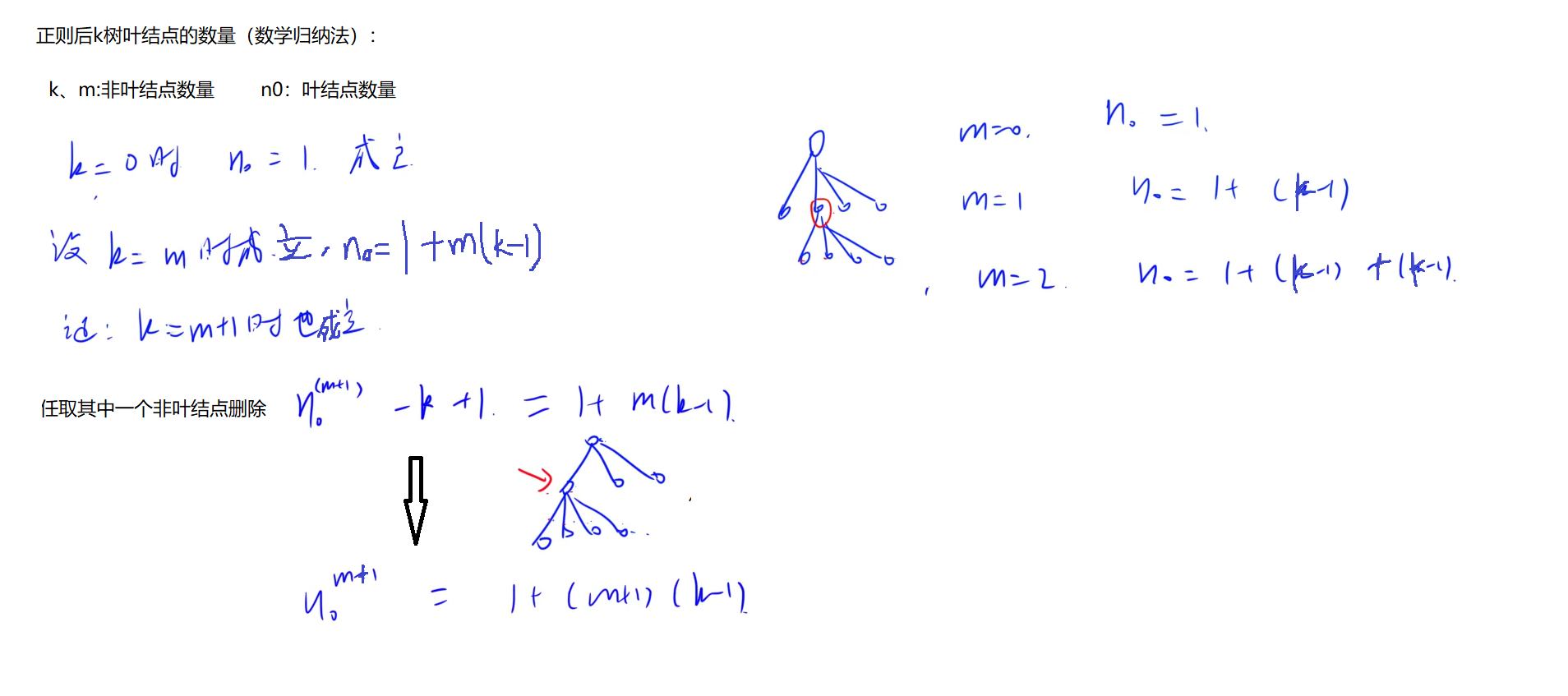
-
顺序存储结构可知,是堆式存储,2x左儿子,2x+1右儿子那种存储结构。
-
2020-4题中,“中序遍历”写错了,应该是森林的后序遍历。
-
押题:AcWing 18 、AcWing 19

