2.5 CRC校验及其实现
一、CRC(循环冗余校验码)校验的基本原理:
原理
和其他校验码相同, 在有效信息位的后面增加校验位,是的校验码具有检错和纠错能力。
CRC不同于奇偶校验,信息位(设为k位)和校验位(设为r位)之间的关系为: N=k+r<=2r−1
一共设置r个校验位,那么r个校验位一共能够表示出2r种状态。
其中只有一种状态对应没有错误,因此还有2^r-1种错误状态, 错误状态的数量一定要大于等于整个校验序列的位数(k + r)
crc可以校验多位出错,并且当只有一位出错时可以纠正它
二、生成多项式 G(x)
(1)定义
生成多项式是收发双方约定的一个(r+1)位的二进制数,发送方利用G(x) 对被校验的信息进行模二的除法运算,以此来生成校验码序列。
接收方也用生成多项式G(x)对收到的编码多项式也做模2的除法运算,以此来检测和定位发生的错误。
(2)G(x)应该满足的条件:
- 最高位和最低为必须为1
- 当被传送信息(CRC码)任何一位发生错误的时候,被生成多项式做除后应该使余数不为0
- 不同位发生错误的时候,模2除运算后的余数是不同的;(以此来区分不同错误)
- 对于不为0的余数继续进行模2除运算应使余数循环。
常见的生成多项式:
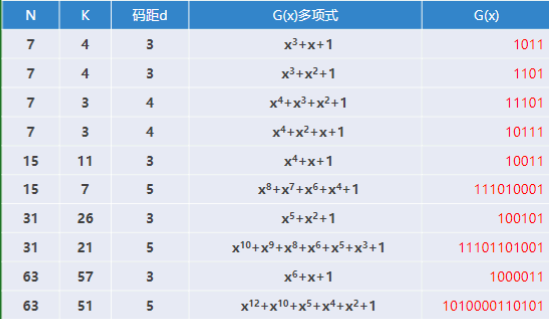
根据不同的K和d来选择合适的G(x)多项式;
三、模2除运算:
(1) 定义
从字面上可理解为二进制下的除法,模2除法与算术除法类似,但每一位除的结果不影响其它位,即不向上一位借位,所以实际上就是异或;
(2)规则
加/减法运算: 亦或运算,加不进位,减不借位;
模二除法: 按模2减,求余数部分,不借位;
上商原则:
1、部分余数首位位1时,商为1,减去除数;
2、部分余数首位为0时,商为0,减0;
3、当部分余数的位数小于除数的位数时,该余数即为最后的余数;
例如:
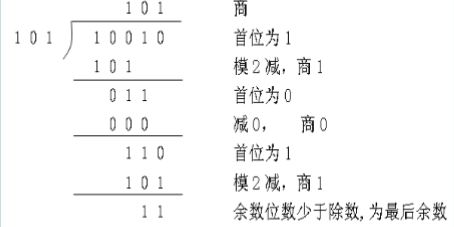
四、CRC编码方法:
推荐一个B站视频,直观讲解了手算和系统中的硬件表达,演示的很好: https://www.bilibili.com/video/BV1V4411Z7VA?from=search&seid=2286647576875784146&spm_id_from=333.337.0.0
步骤
1、根据校验信息位的长度k,按照k+r<=2r−1的关系确定校验位r的位数。
如对4位信息位1100进行CRC编码,根据关系求得rmin=3
2、根据r和生成多项式的选择原则,选择位数位r + 1的生成多项式 G(x) = 1011
3、被校验信息Q(x)逻辑左移r位,得到Q’(x)
也就是原本四位的信息位1100,变味了七位1100000
4、对Q‘(x)按模2除法法则除G(x), 求CRC编码种的r位校验信息
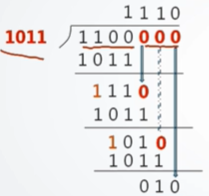
5、用除得的余数替换Q’(x)的最后r位得到对应的CRC编码
Q’(x)原本为1100000,替换后变为1100010,替换后即为最后得到的CRC编码
五、CRC的检错与纠错
(1)检错
发送方将编码发送出后,接收方会利用与发送方相同的生成多项式对收到的序列做模2的除法;
例如对之前举例得到的CRC编码做检验
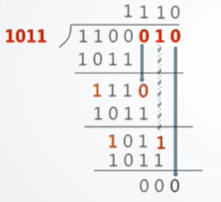
余数为0说明没有发生错误
如果序列在传输过程中发生错误,那么我们按照模2除法一步一步做,最终会得到一个不为0的余数。
如图加入之前的CRC编码接受出现错误变为1100110;
则进行模2除法:

最终的余数变为了100
不同位出现错误最终得到的余数时不同的;
假设接受到的错误编码变为1101010
继续模2除法

最终的余数变为了011
编码不同位数出错对应的余数:
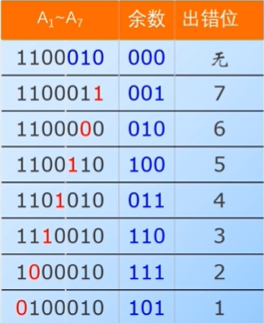
虽然不同位数出错的余数没啥规律,但是不同位数出错对应的余数是不一样的;
(2)一位出错的情况下余数的循环特征及改错:
若收到编码并对编码做关于G(x)的模2除操作后,若余数不为0,则将余数左边添0并且继续对G(x)做模2除操作,得到的余数对应的出错位置,正好是第一次余数对应出错位置的左移;
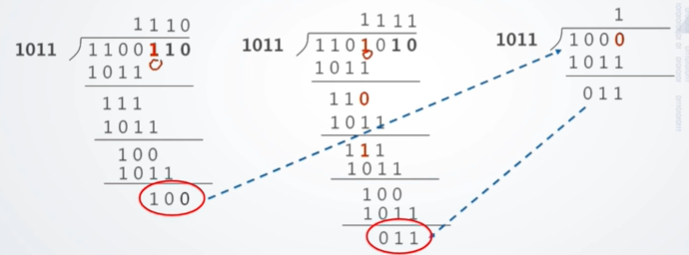
余数为100时查表得第五位出现错误,将100左边添0继续模2除,求得余数为011,查表得是第四位出现错误。
发现这个规律后,只要知道第一位出错时对应出现的余数,然后将收到的错误编码,不断的对余数模2除和将编码左移。直到模2除出现的余数和首位出错时出现的余数相同,这就说明我们已经将错误位移到首位了,然后对首位做亦或操作纠错。之后还要不断的进行对余数模2除和将编码左移,直到出现的余数和纠错过程第一次出现的余数相同时,纠错过了的编码完成了复位。
具体流程建议阅读: https://blog.csdn.net/limaodx/article/details/116559204
当位数增多时,循环码校验能有效降低硬件代价,因此被广泛的使用。

