一、邻接矩阵
int w[5010][5010]; //w[i][j] 表示从节点i到节点j的路径权值
int u, v, d; //起点和终点
scanf("%d%d%d", &u, &v, &d);
w[u][v] = d; //存储边权
二、边表
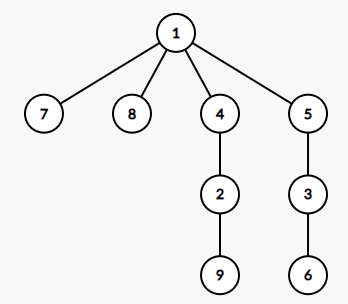
首先存储从x到y的边
编号 x y
1 1 4
2 1 5
3 1 7
4 1 8
5 2 4
6 2 9
7 3 5
8 3 6
然后优化:
建立空间为n的索引表
起始边 结束位置
1 4
2 6
3 8
然后,边表里面只存储y(终点)
三、邻接表
在一个有n个点和m条边的图结构中,把边分为n类
第x类由“从x出发的所有边”构成
vector<int> w[10010];
blabla.....
int u, v;
scanf("%d%d", &u, &v);
w[u].push(v);
直接开vector来存储节点x的第y条邻边即可
四、前向星
前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了。
五、链式前向星
如果说邻接表是不好写但效率好,邻接矩阵是好写但效率低的话,前向星就是一个相对中庸的数据结构。前向星固然好写,但效率并不高。而在优化为链式前向星后,效率也得到了较大的提升。虽然说,世界上对链式前向星的使用并不是很广泛,但在不愿意写复杂的邻接表的情况下,链式前向星也是一个很优秀的数据结构。 ——摘自《百度百科》
int head[N], ver[M], edge[M], Next[M], tot;
void add(int x, int y, int z) {
ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
}

