第一章 概率与计数
尽管概率普遍存在于科学与日常生活中, 但它可能是反直觉的. 如果我们在不知道正确与否的情况
下依靠直觉, 就会出现预测不准确或过于自信而带来严重风险.本书旨在于搭建一个有原则的量化
不确定性和随机性的逻辑框架来介绍概率学.
1.1 为什么要学习概率论
广泛应用
Math is the logic of certainty. Statistic is the logic of uncertainty.
概率论在很多领域都有广泛应用, 它为理解差异、噪声中的分离信号以及复杂现象的建模等提供了一种工具.
避免潜在错误的几种方法
-
数值模拟 : 概率论的魅力在于, 常常可以通过模拟实验来研究问题. 可以运行程序来计算和模拟例子.
-
生物危害 : 研究中常见的错误对于理解什么是概率的合理推理有着很重要的作用. 本书中常见错误称为
生物危害(Biohazards), 用-ω-表示. -
完整性检查 : 当通过一种方法解决问题后, 我们常会用另一种方法解决同一的问题, 或者检验答案在
简单和极端的例子(simple and extreme cases)中的合理性.
1.2 样本空间
概率论的整个框架是建立在 集合 的基础上的. 假设做一个实验, 实验结果是所有可能结果构成集合中的
一个. 在实验前, 我们不知道结果; 实验后结果会具体化为实际的结论.
定义1.2.1 样本空间和事件
一个实验的 样本空间 S 就是这个实验可能出现的所有结果的集合.
Sample space is the set of all possible outcomes of an expriment.
事件 A 是样本空间S的一个子集(subset of sample space).
事件 A发生 当且仅当A中的某个结果实际出现.
(集合让概率从模糊的语言描述->可以进行精确的数学计算)
集合相关
一个实验的样本空间可能是有限的,可数无限的或不可数的(可以参考知乎解释 ). 当样本空间有限时, 我们可以将样本可视化为圆点.
图中每个圆点代表一个实验结果, 一个事件就是一些圆点的集合.
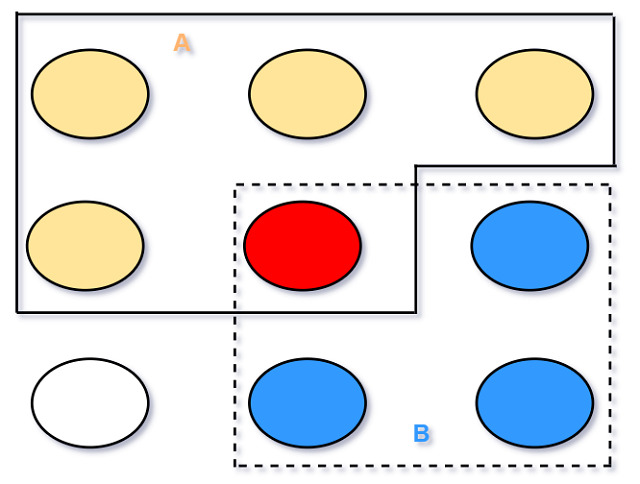
做一次实验就等同于从S中随机选取一个圆点. 如果所有圆点质量相同, 那么每个圆点被抽中的可能性相同.
(概率的朴素定义); 1.6节给出每个圆点被抽中的可能性不同时的概率的一般定义.
集合论中的运算为表达和处理事件(subset)提供了丰富的语言. 例如S代表样本空间, A,B⊆S表示事件.
-
A∪B : 事件发生当且仅当A,B中至少有一个发生.
-
A∩B : 事件发生当且仅当A,B同时发生
-
Ac : 事件Ac发生当且仅当事件A不发生
-
德摩根率 : (A∪B)c=Ac∩Bc, (A∩B)c=Ac∪Bc
两个事件至少其一发生的反面是两个事件都不发生; 两个事件都发生的反面是两个至少其一不发生.
例1.2.2 掷硬币
掷一枚硬币10次, 正面用1表示反面用0表示, 结果可以用数列(s1,s2,…,s10)
表示, 其中si∈0,1. 样本空间S为所有可能数列的集合. 用集合表示下面的事件 :
-
设A1为一个事件, 表示第一次掷硬币的结果为
1, 代表集合如下
A1=(1,s2,…,s10):sj∈0,1且2≤j≤10.
这是样本空间的一个子集, 所以可能看为一个事件. 同样可以设Aj为事件第j次掷硬币的结果为1.1≤j≤10. -
设B事件表示至少有一次掷硬币的结果为
1, 可用如下集合表示
B=⋃10j=1Aj -
设C事件表示所有掷硬币的结果都为
1, 用集合表示为
C=⋂10j=1Aj -
设D事件表示至少有两个连续的
1, 用集合表示为
D=⋃9j=1(Aj∩Aj+1)
至少有1件事情发生 : ∪, 类似于||; 所有事件均发生 : ∩, 类似于&&.
例1.2.3 任意抽取一张纸牌
从标准的52张纸牌中任意抽取一张. 此时样本空间S为全部52张牌的集合.
(52个质量相同的圆点, 每个对应一张牌).

考虑下面4个事件 :
-
A: 点数是
A. -
B: 颜色为黑色.
-
D: 花色为方块.
-
H: 花色为红桃.
我们可以通过事件A,B,D,H构造其他事件. 例如事件A∩H: 抽取的纸牌是红桃A;
A∪D∩H: 抽取纸牌是红色或者点数为A; (D∪H)c=Dc∩Hc=B.
还有很多事件可以通过样本空间定义, 样本空间有52个样本, 问题涉及事件多达252≈4.5∗1015
另一方面, 纸牌为黑桃无法用现有事件表示, 因为这几个集合无法细致到区分黑桃和梅花;
抽到纸牌为🤡也无法用现有事件表示, 这超出了我们的样本空间.
事件与集合
如前面的例子所示, 事件可以用语言或集合符号描述. 通常语言描述更容易理解, 而集合符号更容易操作.
设S为样本空间, sactual为实际实验结果. 下面给出语言描述和集合符号之间的转换表.
| 语言描述 | 集合符号 |
|---|---|
| 事件 | |
| 样本空间 | S |
| s是一个可能的结果(元素) | s∈S |
| A为事件 | A⊆S |
| 事件A发生 | s actual ∈A |
| 必然发生的结果 | s actual ∈S |
| 根据已有的事件得到新事件 | |
| 事件A或事件B发生 | A∪B |
| 事件A与事件B同时发生 | A∩B |
| 事件A不发生 | Ac |
| A或B发生,但不同时发生 | (A∩Bc)∪(Ac∩B) |
| 事件A1,A2,…,An至少有一个发生 | A1∪…∪An |
| 事件A1,…,An均发生 | A1∩…∩An |
| 事件间的关系 | |
| 事件A含于事件B | A⊆B |
| A与B不相容 | A∩B=∅ |
| A1,…,An是样本空集S的一个划分 | A1∪…∪An=S,Ai∩Aj=∅,i≠j |
1.3 概率的朴素定义
历史上, 概率最早定义为使事件发生的所有可能的方法数除以试验所有可能的结果数(古典概率).
这种定义依赖于很强的假设, 称其为 朴素定义 .
1.3.1 朴素的概率定义 naive defination of probability
假设一个试验的样本空间为有限集合S, 设A为这个试验的一个事件, 事件A概率表达如下:
Pnaive(A)=|A||S|=会导致A的结果数量S中总共的结果数量
在点空间中, 朴素定义下的概率就表示事件中圆点占所有圆点的比例.
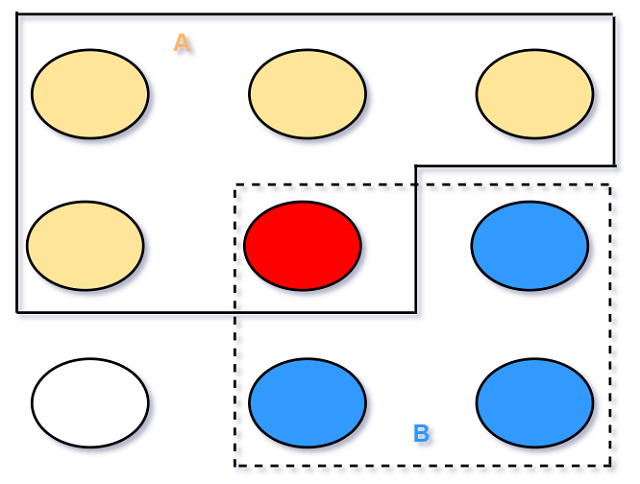
Pnaive(A)=59,Pnaive(A∪B)=89
一般来说, Pnaive(Ac)=|Ac||S|=|S|−|A||S|=1−|A||S|=1−Pnaive(A).
我们在1.6节将看到关于补集(Ac)的很多结论在概率论中同样适用, 不限于概率的朴素定义. 当我们试图
求一个事件的概率时, 一个策略是先考虑是直接确定事件本身的概率容易还是确定它的补集的概率更容易.
朴素定义有很强的限制性, 它要求样本空间S有限且每个样本具有相同概率. 在没有任何推断和论证就直接使用
朴素定义有时会给出荒谬的概率, 甚至自相矛盾 : “火星上有生命这个事件只有两种可能, 发生或不发生. 所以
火星上有生命的概率是50%. 同时也会得到火星上有智慧生命的概率也是50%. “ 但由1.6节介绍的概率性质
可以证明, 后者的概率应该严格小于前者的概率. 但在一下几种问题中, 朴素定义是适用的:
-
当问题存在对称性使得结果等可能出现时. 比如一个公平硬币正反的概率均为50%.
-
当把试验的每个不同结果设计为具有相同可能性时. 例如对样本随机抽取获得一个 简单随机样本. 虽然
这在现实中很难实现. -
当朴素定义被作为一个有效的 零模型 (统计中的一种模型)时.
1.4 如何计数
计算一个事件A的朴素概率涉及事件A和样本空间S的样本圆点数目的计数. 本节介绍一些基本计数方法, 更多
方法可以参考组合学的书籍.
1.4.1 乘法原则
考虑一个复合试验, 由两个子试验A和B构成. 假设试验A有a种可能结果, 每种结果都对应于B
的b种可能结果.那么这个复合试验的结果共有ab种可能结果.
可以用树状图 tree diagram考虑.
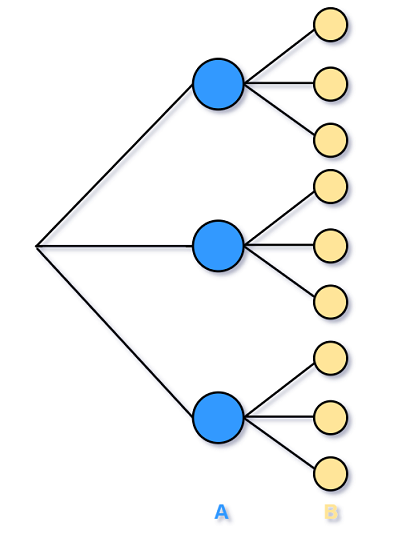
上图复合试验共有3∗3=9种结果.
1.4.2 生物危害 -ω-
通常很容易想当然认为试验是有先后顺序的, 但乘法原则并没有要求试验A必须在试验B之前进行.
例1.4.3
假设Y某正在购买一瓶无糖饮料, 有可口可乐C和雪碧S两种选择, 有原味O、香草V和香蕉B三种口味可选.
决定过程可以用树状图表示.
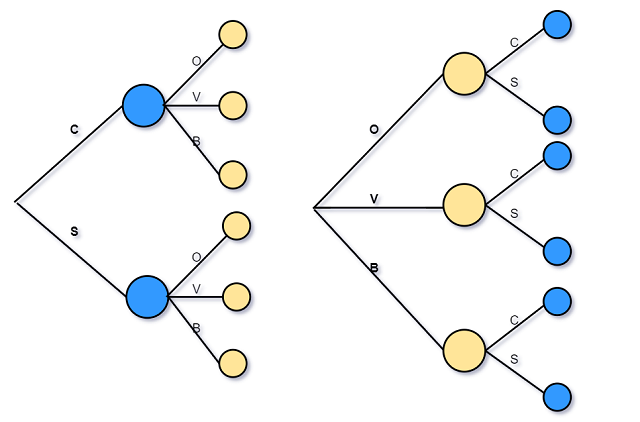
由乘法原则, 共有2∗3=6种选择, 这是较简单的示例, 却值得仔细思考以至推广为更为复杂的情况.
之后遇到的复杂问题在已知空间无法绘制树状图, 但概念上有着相同思路. 这里有一些值得注意的问题:
-
无论先决定品牌类型还是口味类型, 试验共有2∗3=3∗2=6种可能.
-
对于乘法原则, 可口可乐和雪碧对应的口味是否相同是无关紧要的, 重要的是都有
3种可选的口味.
先假设Y某某天共买了两瓶无糖饮料, 由乘法原则可知, 该复合试验共有62=36种可能组合结果.
但如果只需关注这天喝了何种类型的饮料, 而不在乎喝的顺序, 则此时(CO,SB)和(SB,CO)之间没有区别.
那么所有可能是否是62/2=18种? 不是的, 因为对于(SB,SB)这类情况只占可能组合的一项.
所以应分别考虑两瓶饮料相同和不同的情况. 不同饮料的所有组合 : 6∗5/2=15种; 相同饮料的
所有组合:6种. 所以共有21种可能组合. 注意之前36种组合出现可能相同, 此时21种组合出现可能不同.
例1.4.4 子集
一个含n个元素的集合有2n个子集, 包括∅和集合本身. 这符合乘法原则, 因为依次考虑每个
元素的可能结果, 每个元素都有两种可能.(树状图为完美二叉树)
许多概率和统计试验都可归为有放回抽样和无放回抽样, 而运用乘法原则可以得到两种抽样的公式.
定理1.4.5 有放回抽样
考虑从n个个体中抽取k个样本, 有放回的一次选一个(已被选的下次可以再被选). 此时有nk种可能结果.
定理1.4.6 无放回抽样
任是考虑从n个个体中抽取k个样本, 无放回地一次选一个(已被选的不会再次被选). 有n(n−1)…(n−k+1)
种可能结果.
对于无放回问题, k≤n, 而对于有放回问题则没有这个限制.
计数以计算概率
定理1.4.5和定理1.4.6都是关于计数的, 在运用朴素概率定义时, 可以用来计算概率.
例1.4.8 生日问题
一个屋子里有k个人, 假设每个人的生日都等可能的为1年365天中的一天(不考虑2月29日的情况),
且每个人的生日都是独立的(没有双胞胎之类的情况). 屋内有两个及以上的人在同一天过生日的概率是多少?

共有365k种方法给房间里的每个人分配生日, 可以看作在365天里有放回地抽取k天. 因为抽取每天的情况
都是等可能的, 所以可以应用概率的朴素定义.
直接考虑事件至少有两个人生日相同的数目想想就让人头大, 相反我们可以考虑事件的补集 : k个人两两
生日均不相同的数目, 等同于从365天中无放回的选取k天, 所有可能情况为365∗364∗…∗(365−k+1).
P(没有人生日相同)=365∗…∗(365−k+1)365k
所以至少有两个人生日相同的概率为:
P(至少有两人生日相同)=1−365∗…∗(365−k+1)365k
k=366时, 肯定至少有两个人生日相同(鸽巢原理). 但出人意料(反直觉)的时, 即使人数比365小很多, 也会
有很大概率至少两个人生日相同. 当k=23时就有50%的可能至少有两个人生日相同. 这是因为如果有23
人, 那么构成\tbinom{23}{2} = 253对, 每一对都有可能生日相同, 这已经很接近365了.
1.4.9 -ω- 标记对象 label
从人群中进行抽样是统计学中的基础概念. 其中, 将人群中的人或对象进行标记是非常重要的. 例如, 瓶子里
有n个球, 即使这些球看起来一模一样, 依然可以假设将它们用1至n进行标记(为每个对象分配唯一ID进行区分).
与之相关的例子是莱布尼兹在一个看似简单的问题中犯过的启发性错误.
1.4.10 莱布尼兹错误
如果掷两个骰子🎲, 点数之和为11的可能性大还是为12的可能性大?

将两个🎲标记为A和B, 将投掷每个🎲看作一个子试验. 结果用有序对(A的结果, B的结果)表示.
由乘法原则知, 试验共有36种结果, 且是对称等可能的. 其中(6,5)和(5,6)两种情况和为11,
而只有(6,6)一种情况和为12.所以结果11和12的概率为1/18和1/36.
然而莱布尼兹错误认为11和12的可能性相同. “掷出11点和掷出12点的可能性是相同的, 因为11和12都只有一种情况才可能出现”. 这里莱布尼兹犯的错误就是他没有把两个🎲看成
是两个不同的对象, 认为(5,6)和(6,5)是一样的.
(把所有情况枚举都知道结果, 莱布尼兹没有尝试’伟大’的枚举法)
如何避免莱布尼兹的错误? 首先, 如 1.4.9 -ω-, 我们应该给每个对象做标记将它们设定为不可区分的
(数字, 字符, 颜色都可); 其次通过计数来计算概率前要思考朴素定义此时是否适用.
1.4.2 重复计数(overcounting)的调整
在许多计数问题中, 直接对每一种可能性计算且只计算一次是困难的. 如果可以把每一种情况都刚好
计算c次, 那么可以通过将总数除以c来进行调整.
例1.4.11 委员会和小组
考虑一个由4人构成的小团队
\;a) 将2人组成委员会, 有多少种选法?
\;b) 将4人分成每两人一组, 有多少种选法?
首先标记对象(label), 4个人编号 : 1, 2, 3, 4.
\;a)
-
可以用枚举法 : 标号后所有情况为
12,13,14,23,24,34. 共有6中可能. -
也可用
乘法原则 + 重复计数调整. 由乘法原则, 选第一个人时有4种选择, 选第2个人时有3种选择,
总数为12. 但2人成组没有顺序, 所以把所有情况都算了两次(如12, 21), 总数除以2得到6种分法.
\;b) 可用枚举法; 在a)选择2人成委员会, 另外2个人自然成一组. 但2个组之间没有顺序关系,
所以把所有情况计算了2次(如{(1,2),(3,4)}和{(3,4),(1,2)}, 所以总数除以2得到3种分法.
二项式系数 binomial coefficient
计算从一个集合中选取固定个数子集的所有可能数. 例如从n人中选取k人组成委员会, 集合S和子集A都
不考虑顺序. 相当于不考虑顺序且无放回抽样的可能数.
定义1.4.12 二项式系数
对于任意非负整数k和n, 二项式系数\tbinom{n}{k}, 读作”n选k”, 表示大小为n的集合中存在大小为
k的子集个数. 二项式系数\tbinom{n}{k}也成为组合数.
定理1.4.13 二项式系数计算公式
\; \; k\le n时, \tbinom{n}{k} = \frac{n(n-1)…(n-k+1)}{k!} = \frac{n!}{(n-k)!k!}
\; \; k\gt n时, \tbinom{n}{k} = 0.
\; \;证明 : 设A为集合且|A| = n。 A的任意一个子集最多n个元素. 因此对于k\gt n,
不存在这样的子集, \tbinom{n}{k} = 0. k\le n时, 首先考虑无放回且考虑顺序的情况, 共有
n(n-1)…(n-k+1)种可能(乘法原则), 而这里子集不考虑元素顺序, 所以对每种集合重复计算了k!次,
除以k!得到正确解.(重复计数的调整).
1.4.14 -ω-
二项式系数\tbinom{n}{k}由阶乘定义, 虽然负数阶乘没有定义, 但当k\gt n时认为\tbinom{n}{k} = 0.
例1.4.16 字符排列
LALALAAA中的字母有多少种排列可能?
\;\;在8个位置为5个A或3个L确定位置即可, 且不考虑顺序, 所以有
\;\;\tbinom{8}{5} = \tbinom{8}{3} = 56种.
那么单词statistics中字母有多少种排列可能呢?
-
首先在
10个位置中确定s的位置, 接着在剩余7个位置中确定t的位置, 接着确定i,a的位置. -
先不考虑重复计数, 共有10!种可能, 接着除以重复计算的3!3!2!, 因为
3个s之间没有区别.t,i同理.
于是有\tbinom{10}{3} \tbinom{7}{3} \tbinom{4}{2} \tbinom{2}{1} = \frac{10!}{3!3!2!} = 50400种排列方法.
例1.4.17 二项式定理
\;\;(x + y)^n = \sum_{k=0}^n \tbinom{n}{k}x^ky^{n-k}
应用概率朴素定义时, 很多问题可以通过二项式定理解决.
例1.4.18 扑克中的”对子”
从洗好的52张牌中抽取5张, 如果有3张牌点数相同, 另外2张牌点数相同, 不考虑顺序, 就称作对子(fullhouse).则在扑克牌中出现对子的概率是多大呢?

\;\;解 : 根据对称性, 每个牌被抽中可能性相等. 从52张牌无放回不考虑顺序选取5张, 有\tbinom{52}{5}种
可能, 考虑这其中有对子的可能, 运用乘法原则, 首先考虑3张相等的点数, 从4种花色中选3张, 接着考虑2张相等的点数, 从4种花色中选取2张. 所以 :
\;\; P(对子) = \frac{13\tbinom{4}{3}12\tbinom{4}{2}}{\tbinom{52}{5}} \approx 0.00144
例1.4.19 Newton-Peps问题
牛顿(Newton)曾被一个对赌博问题很感兴趣的名为Peps的人提问, 如下哪个事件出现概率最高?
-
A: 掷6次骰子至少出现1次6点. -
B: 掷12次骰子至少出现2次6点. -
C: 掷18次骰子至少出现3次6点.
由对称性可知, 对于这3个试验朴素概率定义都使用. 每次掷🎲结果的概率均为\frac{1}{6}.
-
A: 计算A^c(掷6次骰子没有出现1次6点)更容易. 每次掷🎲不是6点的可能性是\frac{5}{6}.
\;\;P(A) = 1 - \frac{5^6}{6^6} \approx 0.67 -
B: 对事件B^c计数, 试验共有6^{12}种结果, 没有1次6点的情况有5^{12}种; 只有1次6点:
首先确定是哪一次, 剩余11种从1~5中选择, 有\tbinom{12}{1}5^{11}中情况.
\;\;P(B) = 1 - \frac{5^{12}+\tbinom{12}{1}5^{11}}{6^{12}} \approx 0.62 -
C: 还是对C^c计数, 即掷🎲18次, 出现0, 1, 2次6点情况分别有5^{18}, \tbinom{18}{1}5^{17}, \tbinom{18}{2}5^{16}.
\;\;P(C) = 1 - \frac{5^{18} + \tbinom{18}{1}5^{17} +\tbinom{18}{2}5^{16}}{6^{18}} \approx 0.60
牛顿同学用类似的运算得出了正确解, 但他的直观论证是无效的, 因其论证过程
不是建立在🎲是均等的前提之下.(结果概率均等)
下面介绍一个简洁且富有技巧的计数示例, 但结论很少适用于朴素概率定义上.
Bose-Einstein
有放回地从n个对象中抽取k个, 一共有多少种方法? 如果不考虑顺序(只关心每个对象被抽取的个数,
不关心其被抽取的顺序), 一共有多少种方法?
考虑顺序时, 由乘法原则可知共有n^k种方法; 不考虑顺序时问题变得很复杂, 下面通过一个同构问题(同一
问题在不同情境下)来解决它.
考虑这样一个问题: 将k个无法区分的粒子放进n个可区分的盒子里. 共有多少种方法?
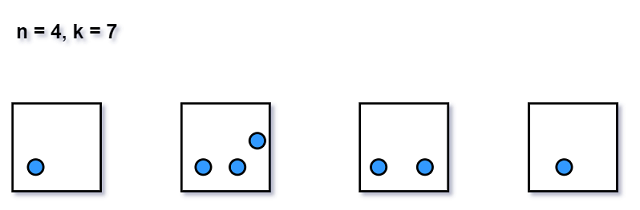
不同情况的区别在于不同盒子里粒子的数目. 可以进一步简化问题的编码, 任意的情况可以用|和O表示示.

所有序列都要以|作为开头和结尾, 中间有n-1个|和k个O. 每个序列于每种情况一一对应.对于序列,
我们只需要在n - k + 1个位置中选择k个位置放置O, 所以共有\tbinom{n-k+1}{k} \tbinom{n-k+1}{n-1}种可能.
这被称为Bose-Einstein值,因为物理学家玻色(Bose)和爱因斯坦(Einstein)在1920年做了不可区分
粒子的相关研究,用他们的想法成功预测(70年后被实验证实)了一种叫做Bose-Einstein condensate的物质状态.
关联到原来的问题, 每个盒子对应可区分的n个对象, 每个粒子对应不考虑顺序的k次选择.
1.4.21 -ω-
除极特殊情况外, Bose-Einstein结果不能应用于朴素概率定义中. 一般只考虑每个样本被抽取的次数
而不考虑其顺序的情况非常少见.
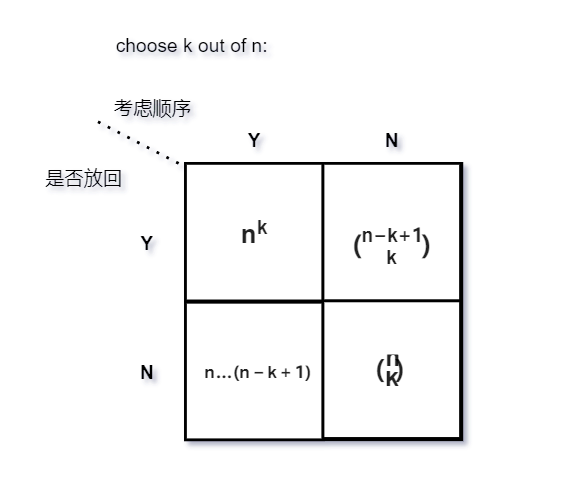
sampling table
从n个样本中选取k个 :
1.5 讲述证明 story proofs
讲述证明(story proofs)是指通过解释进行证明. 对于计数问题, 它意味着通过两种不同的方法计算
同一种问题. 一个讲述证明通常会避开繁琐的计算, 在代数证明的基础上进一步解释其结果. 一个讲述
证明同样是一个完全有效的数学证明. 下面给出几个讲述证明的例子.
(story proofs是个人觉得本书中最有趣和最优美的解释方式)
例1.5.1 选择补集
对于任意非负整数n和k, 满足k\le n, 有
\;\;\tbinom{n}{k} = \tbinom{n}{n-k}
该结论在代数上很好证明(二项式展开即可), 但用story proofs更容易从直观上理解.
\;\;story proofs: 考虑从n个人中选出k个人组成委员会, 一种方式是直接确定k个人, \tbinom{n}{k}种结果;
另一种方式是确定出n-k个人不再委员会中, \tbinom{n}{n-k}种结果.
例1.5.2 团队队长
对于任意n和k, 满足k\le n, 则有
\;\;n\tbinom{n-1}{k-1} = k\tbinom{n}{k}
\;\; story proofs: 考虑从n个人中选出k个人组成一个团队, 且团队中有一人为队长. 此时可以先选出队长,
再从剩余的n-1人中选出k-1个人组成队员, 写作左边的等式; 等价地, 也可以先选出k个人组成一个团队, 再
从k个人中选取一个人为队长, 写作右边的等式.
例1.5.3 范德蒙恒等式
关于二项式系数的一个著名关系叫做范德蒙(Vandermonde)恒等式 :
\;\;\tbinom{m+n}{k} = \sum_{j=0}^{k}\tbinom{m}{j}\tbinom{n}{k-j}
试图将两边二项式系数盲目展开是很愚蠢的. 而使用讲述证明可以清晰漂亮的证明这个等式.
\;\;story proofs : 从m位男士和n位女士中选出k个人组成委员会. 此时共有\tbinom{m+n}{k}种选法, 即
等式左侧. 如果委员会中有j位男士, 则委员会中必有k-j位女士. 把所有j可能出现的情况进行加和得到等式右侧.
例1.5.4 合作伙伴
\;\; \frac{(2n)!}{2^n\times n!} = (2n-1)(2n-3)…3 \times 1
\;\; story proofs : 将2n个人两两组成n对合作伙伴, 共有多少种方法? 下面将证明等式两侧都是对这个问题的
计数. 首先, 给2n个人标号1~2n. 再把2n个人按某种顺序排列, 将第1个和第2个组成一组, 第3个
和第4个组成一组,以此类推. 不考虑n对合作伙伴的顺序也不考虑没对两人的顺序, 此时重复计数了2^n*n!倍;
另一个思路是, 首先对于1号, 他共有2n-1种选择, 然后对于2号, 他有2n-3种选择(如果1号选择了2号,
那3号有2n-3种选择), 以此类推.
1.6 概率的非朴素定义 non-naive defination of probobility
\;\;前面介绍的几种计数方法可以应用于朴素定义的概率计算, 但有很强的限制性 : 要求每个结果等可能且样本
空间有限. 为将概率的概念一般化, 可以自己对定义进行构造 : 首先写下我们认为概念应该如何表现的清单
(数学上清单的内容被称为公理axiom), 然后定义一个概率公式满足我们想要的性质.
\;\;本书余下部分都将使用概率的一般定义, 它只需要2个公理, 但由这两个公理可以推出概率论的一系列结果.
定义1.6.1 概率的一般定义
\;\;一个样本空间包含一个样本空间S和一个概率函数P, 给定一个事件A\subseteq S作为输入, 返回[0,1]
区间上的实数P(A)作为输出. 函数P必须满足如下公理 :
-
P(\varnothing) = 0, P(S) = 1
-
如果A_1, A_2, …是两两不相交事件(对任意i\not= j, A_i\cap A_j = \varnothing), 则有
\;\;P(\bigcup_{j=1}^{\infty}A_j) = \sum_{j=1}^{\infty}P(A_j)
概率具象化
\;\;在圆点空间里, 概率的定义类似质量: 空圆点质量为0, 所有圆点质量为1. 如果存在一堆不重合
的圆点, 可以通过对每个圆点的质量加和得到这堆圆点的质量. 每个圆点的质量可以不同, 也可以有无限
个圆点, 只要它们的质量之和等于1.
\;\;对于不可数的样本空间, 我们可以想象一块泥铺开覆盖一片区域上, 而这块泥总质量为1.
解释概率的两个学派
\;\;满足上述两个公理的任意函数P(将事件映射到区间[0,1])都可以认为是有效的概率函数. 然而这些
公理并没有告诉我们怎样解释概率, 这里存在两种不同的学派:
-
概率学派(
frequentist), 概率是指在进行了大量重复试验后出现某个结果的频率的长期趋势. 例如我们
说一枚硬币出现正面的概率是\frac{1}{2}是指不断重复掷一枚硬币, 应该有50\%的结果是正面朝上. -
贝叶斯学派(
Bayesian), 概率表示对一个事件的相信程度, 所以可以直接对类似”A在这次选举中会赢”或
“被告有罪”这样的假设指定概率, 因为同样的选举和同一个罪行无法不断重复.
\;\;贝叶斯学派的视角和频率学派的视角是互补的, 两者都将有助于增强直觉. 不管从那个视角都可以通过上述
两个公理推导出概率的其他性质, 而这些性质对所有有效的概率函数都适用.
定理1.6.2 概率的性质
\;\;对任意的事件A和B, 概率具有如下性质:
1. P(A^c) = 1 - P(A)
2. 若A\subseteq B, 则P(A)\le P(B)
3. P(A\cup B) = P(A) + P(B) - P(A\cap B)
证明 :
-
1 因为A和A^c不相交, 且A\cup A^c = S, 由
公理2, 有
\;\; P(S) = P(A\cup A^c) = P(A) + P(A^c), 又由公理1, P(S) = 1, 因此P(A) + P(A^c) = 1. -
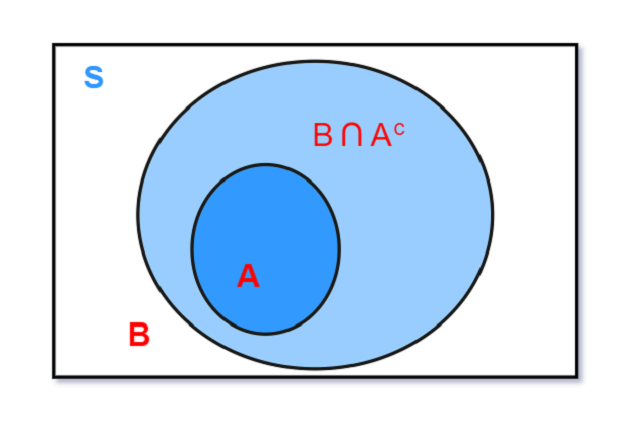
2 如果A\subseteq B, 则可以写作B = (B\cap A^c)\cup A, 这里B\cap A^c表示B集合中与A不相交的部分.
\;\;因为A和B\cap A^c是不相交的, 由公理2:
\;\;P(B) = P(A\cup (B\cap A^c)) = P(A) + P(B\cap A^c)
\;\;又因为概率是非负的(概率函数P\in [0,1]), 所以P(B\cap A^c)\ge 0, 于是P(B)\ge P(A)
- 3 可以参考下面的韦恩图对结果进行直观解释 :
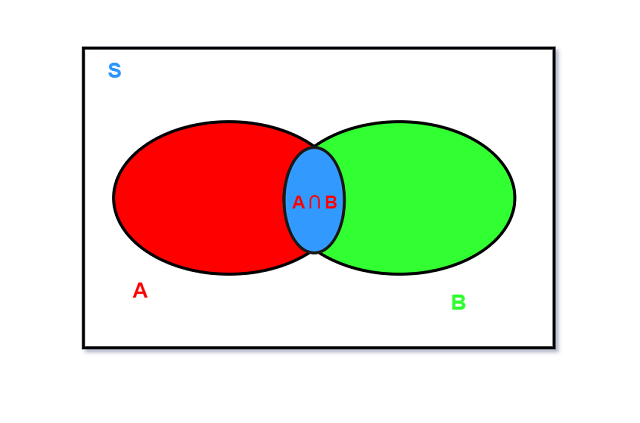
- 3 上图涂色部分代表A\cup B, 但该区域的概率并不是P(A) + P(B), 因为这样就计算了两次A\cap B
的区域. 所以需要减去P(A\cap B)进行修正. 上述只是直观理解, 下面利用公理进行证明.
在证明过程中使用了两个策略:脱节, 将概率的计算形式变换为几个不相交集合的并的形式, 以应用公理2.wishful thinking, 希望证明成立, 即观察在什么情况下等式成立, 并思考对应情况是否正确.
首先把A\cup B写成两个不相交事件A和(B\cap A^c)的并(脱节), 由公理2, 有:
\;\; P(A\cup B) = p(A\cup (B\cap A^c)) = P(A) + P(B\cap A^c)
现在我们希望等式成立(wishful thinking), 即P(A) + P(B\cap A^c) = P(A) + P(B) - P(A\cap B),
也就是P(B) = P(B\cap A^c) + p(B\cap A) , 这个等式显然是成立的(B被A和A^c两个部分), 得证.
容斥原理 inclusion-exclusion
\;\;第三个性质是容斥原理(inclusion-exclusion)的一种特殊情况, 可以推广为求一组事件两两不相交时,
它们的并的概率公式. 前面介绍对于2个事件A和B, 有
\;\; P(A\cup B) = P(A) + P(B) - P(A\cap B)
\;\;对于3个事件, 有
\;\;P(A\cup B \cup C) = P(A) + P(B) + P(C) - P(A\cap B) - P(A\cap C) - P(B\cap C) + P(A\cap B \cap C)
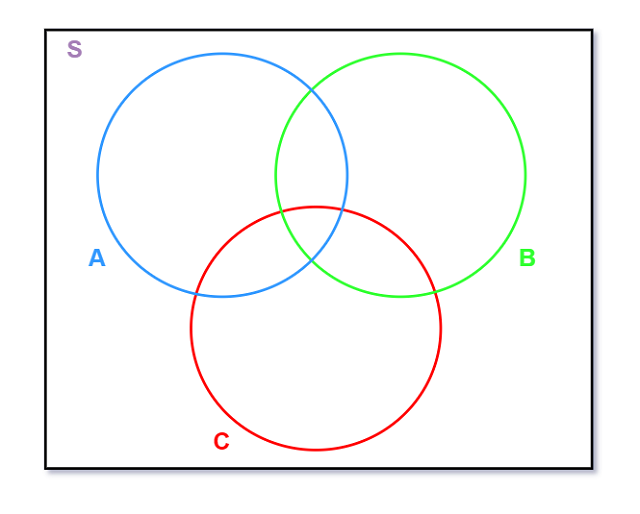
求带颜色圆圈的总面积A\cup B\cup C, 首先将3个部分相加: P(A) + P(B) + P(C), 3个重合区域被加
了2次, 所以要减去P(A\cap B) + P(A\cap C) + P(B\cap C), 中心3个集合重合部分被加了3次又被减了
3次, 所以最后要再加回. 这样就保证区域所有部分都只计算了1遍.
推广至n个事件的情况, 有如下定理
定理1.6.3 容斥原理
\;\;对于任意事件A_1, …, A_n, 有
\;\;P(\bigcup_{i=1}^n A_i) =
\sum_{i} P(A_i) - \sum_{i\lt j} P(A_i\cap A_j) + \sum_{i\lt j\lt k}P(A_i \cap A_j\cap A_k) - … + (-1)^{n+1}P(A_1\cap …\cap A_n)
这个公式可以仅仅通过公理进行证明, 但在第4章介绍一些新方法后可以对其进行更简洁的证明.
蒙特莫特(Montmort)配对问题是一个著名的应用容斥原理的例子.
例1.6.4 蒙特模特配对问题 对称性+容斥原理
\;\;本题两个反直觉的点 :
- 离散的卡片问题
->微积分中连续的e - n
->\infty时, 概率不是趋近0或1, 而是一个常数.
\;\;考虑洗好的n张卡牌, 标记为1到n. 一张一张的翻卡片并同时从1到n喊数. 如果在某个时刻喊出的数
与翻出卡片的数字相同就算赢.(例如第7张卡片的标记也为7). 那么赢的概率是多少?
解:
令A_i表示第i张卡片的标记是i的事件, 所以问题转化为A_1\cup …\cup A_n, 因为只要有1张卡片
数字吻合就赢. 为计算概率使用容斥原理, 首先对所有的i都有,
\;\; P(A_i) = \frac{1}{n}
这可通过朴素概率定义得到, 全样本空间n!, 若第i个位置固定为标号为i的卡片, 其他卡片位置任意, 有
(n - 1)!种排列; 另一种思路是卡片i在任何位置的可能性相同, 所以其恰好在第i个位置的可能性为\frac{1}{n}
\;\;其次
\;\; P(A_i\cap A_j) = \frac{(n-2)!}{n!} = \frac{1}{n(n-1)}. 因为指定i和j在对应位置上, 其剩余的
n-2张牌任意排列. 类似的, 有
\;\; P(A_i\cap A_j\cap A_k) = \frac{(n-3)!}{n!} = \frac{1}{n(n-1)(n-2)}
以此类推.
在容斥原理公式中, 涉及1个事件的有n项, 涉及2个事件的有\tbinom{n}{2}项, 涉及3个事件的有\tbinom{3}{n}项… 由对称性可知, 所有P(A_i)都相等, 且\tbinom{n}{2}项P(A_i\cap A_j)都相等… 表达式可简化如下
\;\; P(\bigcup_{i=1}^n A_i) = \frac{n}{n} - \frac{\tbinom{n}{2}}{n(n-1)} +
\frac{\tbinom{n}{3}}{n(n-1)(n-2)}) - … + (-1)^{n+1}\frac{1}{n!}
= 1 - \frac{1}{2!} + \frac{1}{3!} - … + (-1)^{n+1}\frac{1}{n!}
这与1/e的泰勒级数形式相同, 因此随着n的增大, 赢的概率逐渐逼近1 - 1/e, 约为0.63. 有趣的是, 随着
n的增长, 赢的概率没有趋近0或1. 当卡片增多时, 可能配对成功的位置增加了, 但每个指定位置配对成的概率
减少了, 两股力量相互抵消平衡最终概率接近了1 - 1/e.
1.7 要点重述
概率论提供了一种量化不确定性和随机化的方法. 当一个试验被实施时, 概率就会出现: 所有可能的结果的集合
叫做样本空间, 样本空间的一个子集叫做事件. 事件的语言描述和集合符号之间的转换是非常重要的.
当样本空间有限时, 圆点空间(pebble world)可以帮助我们可视化地理解样本空间和事件. 将每一种可能结果
比作一个圆点, 此时事件就是若干圆点的集合, 如果每个圆点质量相同(等可能), 就可以应用朴素概率,通过计数
来计算概率.
我们也讨论了一些计数方法. 在计算所有可能时, 可以应用乘法法则. 如果不能直接用乘法法则求出, 则可以把
每种可能都计算c遍(重复计数原则), 然后将总数除以c得到正确解.
在使用朴素概率定义时存在一个陷阱, 就是朴素定义隐含或明确假设了等可能性. 通过给每个对象做标记(label)
以精确地区分它们.
跳出朴素概率定义, 可将概率定义为一个作用在事件上, 输出结果在[0,1]之间的函数. 有效的概率函数满足下面
两条公理 :
-
P(\varnothing) = 0, P(S) = 1
-
如果A_1, A_2, \cdots是两两不相交事件(对任意i\not= j, A_i\cap A_j = \varnothing), 那么有
\;\;\;\;P(\bigcup_{i=1}^{\infty}A_i) = \sum_{i=1}^{\infty}P(A_i)
许多有用的性质可以由这两个公理直接推导出来.
下图说明了概率函数如何将事件映射到[0,1]区间上的实数.
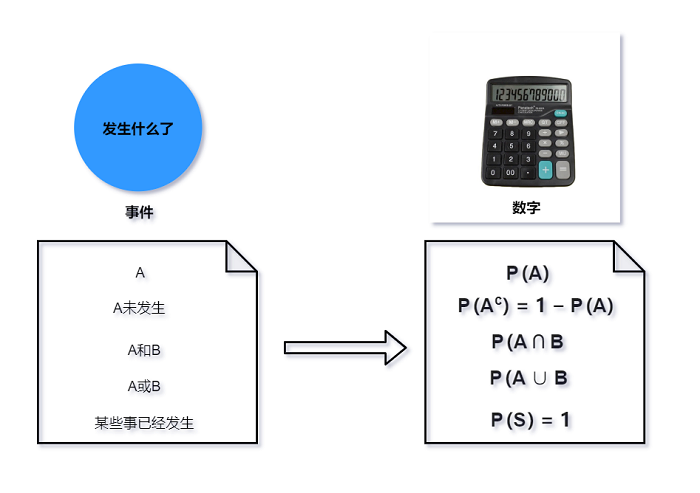
对事件和概率进行区分是很重要的. 前者是集合, 后者是数字. 在一个试验完成前, 通常无法知道特定事件
是否发生. 此时可用概率函数P为其指定概率. 我们可以通过集合运算基于已有事件来定义新的事件以及
这些事件之间的概率相关性质.


%%%%
%%%%%%
tql
Orz!
STO
😀
概括的挺详细的,很有帮助!
谢谢😀