2.1 机器数的特点

（1）为什么要研究机器内的数据表示？

目的： 组织数据，方便计算机硬件的直接使用。

考虑因素：

• 支持的数据类型
• 能表示的数据范围
• 能表示的数据精度
• 存储和处理的代价
• 是否有利于软件的移植

（2）机器内的数据表示

真值： 符号用“+”、“-”表示的数据表示方法
机器数：符号数值化的数据表示方法， 用0和1表示符号

常见的三种机器数：原码、反码、补码。

如：$X = + 1011$

则：$ X_原 = X_反 = X_补 = 01011 $

如：$X = -1011$

则： $ X_原 = 11011，X_反 = 10100，X_补 = 10101 $

负数的反码是原码的数值位取反，负数的补码是其反码再加一。

0的表示：

$ [+0]_原 = 00000 \qquad [-0]_原 = 10000 $
$ [+0]_反 = 00000 \qquad [-0]_反 = 11111$
$ [+0]_补 = [-0]_补 = 00000$

（3）常见机器数的特点：

1、原码：

• 表示简单
• 运算复杂（符号不参与运算，要设置加法、减法器）
• 0的表示不唯一

2、 反码：

• 表示复杂
• 运算相较原码简单（符号位参与运算，只要设置加法器，但符号位的进位要加到最低位）
• 0的表示不唯一

反码运算举例：

$ X = 1101， Y = -1010，求 X + Y $

$ X_反 = 01101, Y_反 = 10101$

    0 1 1 0 1
+   1 0 1 0 1 
--------------------
  1 0 0 0 1 0 
+           1   （符号位的进位要加到最低位）
--------------------
    0 0 0 1 1

$ 所以，X + Y = 00011 $

3、补码：

• 表示复杂
• 运算简单（只需要设置加法器）
• 0的表示唯一

（4）移码

移码用于表示浮点数的阶码，IEEE754中阶码用移码来表示。
移码的定义： $X_移 = X + 2^n$ (X为真值，n为X的整数位位数)

移码的数值位与补码相同，符号位与补码相反；

如 $X = +10101$， $X_补 = 010101$， $X_移 = 110101$

2.2 定点与浮点数据的表示

（1）定点数据的表示：

1. 可以表示小数和整数
2. 表现形式：$X_0 (.) X_1 X_2 X_3 X_4 …X_n (.)$
   ( $X_0$ 为符号位；表示小数的时候，小数点默认放在$X_0$ 和$X_1$之间；表示整数的时候，小数点默认放在数值末尾)
3. 定点小数表示数的范围（以补码为例）：$-1 \le x \le 1 - 2^{-n}$
4. 定点整数表示数的范围（以补码为例）：$-2^n \le x \le 2^n - 1$
5. 不足：数据的表示范围太受限制

（2）浮点数据表示

将数的范围和精度分别表示出来得一种数据表示方法；

1 、一般格式：

任意小数$N$都可表示为：$N = 2^e * m $
(类似于科学计数法的表示方法）
例如：$10101 = 2^{100} * 1.0101$
（e和m都用二进制表示）

其中E为阶码位数，决定了数据的范围（$Es$为阶码的符号位）；
M为尾数的尾数，决定了数据的精度（$Ms$为尾数的符号位）；

不足： 不同的系统可能有不同的浮点数格式的规则，使得数字错误；

2、 IEEE 754 格式

IEEE 754 格式对单精度和双精度数据的表示有统一的描述：

指数采用偏移值，其中单精度的偏移值为127，双精度的偏移值为1023；
偏移值将浮点数的阶码变成非负整数，便于浮点数的比较和排序；

IEEE 754尾数的形式为$1.XXXXXX$，其中$M$部分保存的是$XXXXXX$（1被隐藏了）；
这样可以保留更多的有效位，提高数据表示的精度；

我们以单精度浮点数表示为例细说：

与IEEE 754格式相对应的32位浮点数的真值可以表示为

$N = (-1)^S * 2^{(E-127)} * 1.M$

E和M的取值不同，浮点数表示不同的含义：

1. $E = 0， M = 0$： 表示机器零 （机器数表示$0$的形式）
2. $E = 0， M \neq 0$： 表示非规格化的浮点数
3. $1 \le E \le 254$: 表示规格化的浮点数
4. $E = 255，M = 0$：表示无穷大的数，对应 $x / 0$(其中$x \neq 0$)
5. $E = 255， M \neq 0$: N = NaN, 表示一个非数值，对应$0 / 0$

机器数与真值之间的转换（以32位浮点数为例）：

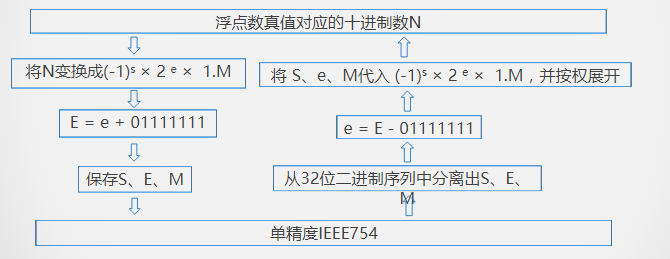
例如：将 $20.59375$ 转换成32位IEEE754格式浮点数二进制

现将十进制数装换成二进制数：
$20.59375 = 10100.10011$

移动小数点，让其成为$1.M$的格式
$10100.10011 = 1.010010011 * 2^4$

得到：
$S = 0， e = 4, E = 100 + 01111111 = 10000011（e要加上偏移量）, M = 010010011$

最终浮点数的二进制表示为：
$0,10000011,01001001100000000000000 = (41a4c000)H$

float类型数据变量不允许位运算操作，因此不能直接对浮点数做位运算来打印二进制表示。

数据和指令在内存中都是以01的方式存储的，计算机并不知道哪个是int，哪个是float，哪个是指令，内存中的数据解释成什么。
因此我们可以人为的指定数据的类型，将float类型的二进制串变为整数类型，再借用位运算打印二进制数；

代码：

#include <iostream>

using namespace std;

int main()
{
    float a = 20.59375;
    printf("float数为：%f\n", a);

    /*    打印浮点数二进制    */
    printf("二进制表示为：");
    int *f = (int*) (&a);           // 将指向float类型的指针强制装换为指向int类型的指针

    for(int i = 31;i >= 0;i --) 
    {
        printf("%d", *f & (1 << i) ? 1 : 0);
        if(i == 31) printf(", ");
        if(i == 23) printf(", ");
    }
    puts("");

    /*    打印浮点数十六进制    */
    printf("十六进制表示为：%x", *f);

    return 0;
}

对$20.59375$的打印结果如下：

与刚才推导结果相同。