数据结构初步

线段树

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

就像这样：

作为一种通用且高效的数据结构，它的作用主要体现在 单点修改，区间查询，区间修改 三个方面，

下面，我会向大家介绍这三个操作的实现方式，和一些简单的应用途径。

由底向上的信息传递

这是线段树最基本的操作之一，

其思想是指父节点的储存值可以 被更改或累计 其树叶子节点的值，但要求具有 代表性，或者说是只能传递 带有结合律 的信息

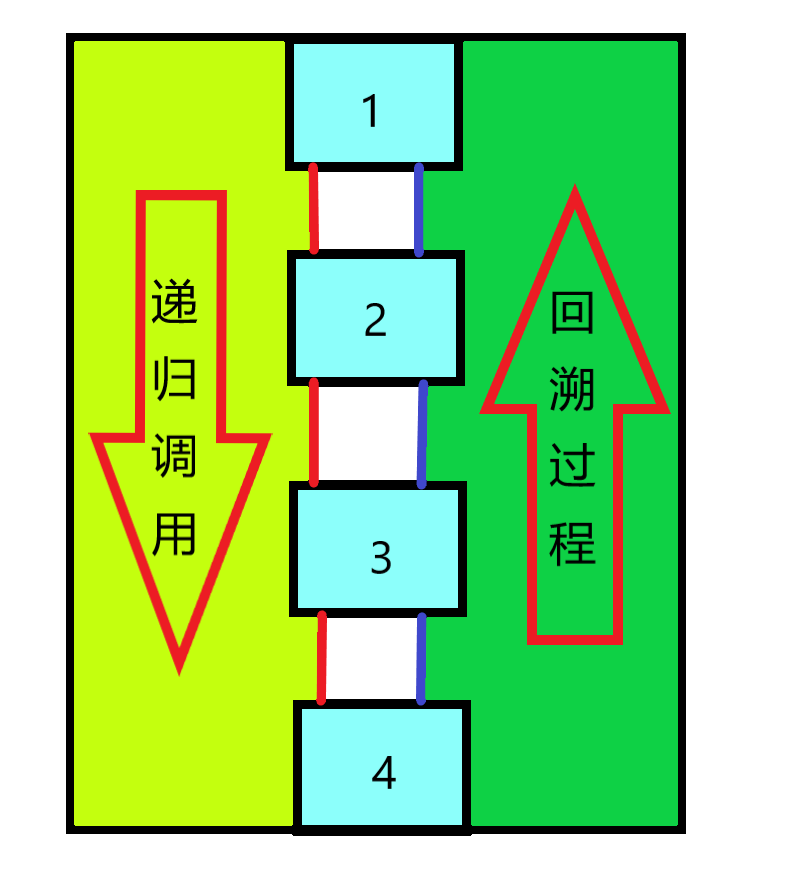
只需要在每一次递归后判断是否会因为子节点的值变化而改变自身就可以了。

因为递归的返回过程是这样的

void pushup(int p) {

    seg[p].dat = max(seg[p * 2].dat, seg[p * 2 + 1].dat);
}

所以每一次更改都只有等到子节点更新完了才能进行，故称为自底向上。

线段树——建树

作为本算法必要的初始条件，建树是最简单的操作…额之一。

只要将每一个区间的信息用递归更新就可以了，当然，要从起点出发

具体步骤包括

1. 确定当前递归区间的左右端点，遍历到叶节点就返回

2. 否则将当前区间折半，继续遍历折半的区间

3. 最后由底向上维护值就可以了

void build(int p, int l, int r) {  
    seg[p].l = l, seg[p].r = r;     // 节点 p 代表区间 [l, r]
    if (l == r) return;             // 叶节点, 不需要赋值
    int mid = l + r >> 1;           // 折半
    build(p * 2, l, mid);           // 左子树
    build(p * 2 + 1, mid + 1, r);   // 右子树

    pushup(p);
}

线段树——单点修改

同样是最简单的操作之一，不过因为一个点的更新，可能会影响其它点的信息，

所以需要将 包括所需更新的点的所有点一并更新

为了方便，依旧建议使用有底向上传递。

具体步骤包括

1. 从上往下找到包括所需更新点在内的所有区间，如果已是叶节点就可以直接返回

2. 更改点信息后依次往上返回，按由底向上的顺序更包括当前更新的点在内的所有区间

void change(int p, int x, int v) {  // 找到 p[x, x] 的叶节点, 再从下往上传递信息
    if (seg[p].l == seg[p].r) {seg[p].dat = v; return;} // 找到叶节点

    int mid = seg[p].l + seg[p].r >> 1; // 取当前区间的中点
    if (x <= mid) change(p * 2, x, v);  // x 属于左半部分
    else change(p * 2 + 1, x, v);       // x 属于右半部分

    pushup(p);                          // 从下往上传递信息
}

线段树——区间查询

这个就没那么简单了。

主要思路是 查询所有查询范围[l, r]覆盖的区间

为了减少篇幅，下面会用抽象的方式帮助大家理解。

用词的释义，有用：查询范围包括在内

1. 查询范围包含了当前节点时直接返回，因为其中的值都是有用的，所以直接输出维护的结果不会影响最后答案

2. 查询范围含有当前节点的左子树，递归左子树，原则一样

3. 查询范围含有当前节点的右子树，递归右子树，原则一样

这个代码实现了查询 $Max$ 的操作

// 区间查询
int query(int p, int l, int r) {    
    // 完全包含, 剩下的子树不用再递归, 直接返回储存的 max 值即可
    if (l <= seg[p].l && r >= seg[p].r) return seg[p].dat;  

    int mid = seg[p].l + seg[p].r >> 1; // 左子树[l ~ mid], 右子树[mid + 1, r]  
    int val = -1e8;                     // 储存最大值
    if (l <= mid) val = max(val, query(p * 2, l, r));   // 递归左子树
    if (r > mid) val = max(val, query(p * 2 + 1, l, r));// 递归右子树
    return val;                         // 返回最大值
}

当然，如果是查询 $sum$ 的话，还会有所不同。

只要相加就可以了

int query(int p, int l, int r)
{
    if (seg[p].l >= l && r >= seg[p].r) return seg[p].sum;

    pushdown(p);

    int mid = seg[p].l + seg[p].r >> 1;
    int sum = 0;
    if (l <= mid) sum = query(p * 2, l, r);     // 左子树的部分
    if (r > mid) sum += query(p * 2 + 1, l, r); // 加上右子树的部分
    return sum; // 直接返回

}

由上到下的信息传递

这个操作的实现需要引入一个重要概念，即懒标记。

其实就是一个暂时不处理，等到需要用到的时候再进行处理的思想。

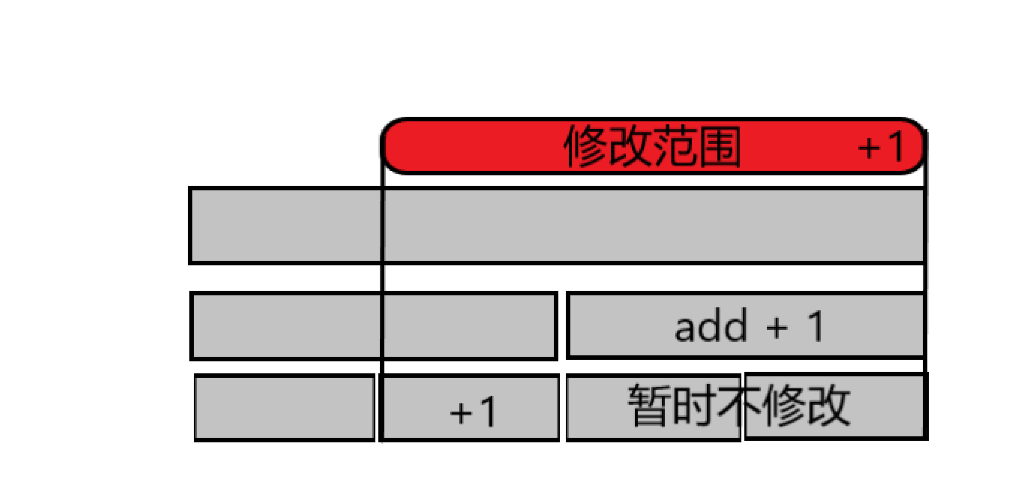
这个代码就实现了 $sum$ 值的维护

void pushdown(int p)// 由上往下传递信息
{
    Smtree &fa = seg[p];
    Smtree &left = seg[p * 2], &right = seg[p * 2 + 1];

    if (fa.add)
    {
        left.add += fa.add;
        left.sum += (left.r - left.l + 1) * fa.add;
        right.add += fa.add;
        right.sum += (right.r - right.l + 1) * fa.add;
        fa.add = 0;
    }
}

线段树——区间修改

这个就是上面思想的具体实现

如果发现当前区间被完全覆盖，就在代表当前区间的节点上做标记，不再往下递归。

如果后续指令需要往下递归，我们在检查 节点 是否有标记，若有标记，就根据标记信息更新 节点 的两个子节点

同时为 p 的两个子节点增加标记，然后清除 p 的标记

void change(int p, int l, int r, int d)
{
    if (seg[p].l >= l && r >= seg[p].r) 
    {
        seg[p].sum += (seg[p].r - seg[p].l + 1) * d;
        seg[p].add += d;
        return;
    }

    pushdown(p);// 由上往下传递信息

    int mid = seg[p].l + seg[p].r >> 1;     // 折半
    if (l <= mid) change(p * 2, l, r, d);   // 左子树
    if (r > mid) change(p * 2 + 1, l, r, d);// 右子树

    pushup(p);  // 由下往上传递信息
}

区间合并

什么是区间合并？

当出现一个同时覆盖左右两个区间的查询，且将两个信息分开算时是错误的，就可以用区间合并解决

也就是合并两个区间的查询结果，只需要定义一个虚拟父亲作为中间过程将结果传递上去就可以了

Smtree query(int p, int l, int r)
{
    if(l <= seg[p].l && r >= seg[p].r) return seg[p];

    int mid = seg[p].l + seg[p].r >> 1;

    if (r <= mid) return query(p * 2, l, r);
    if (l > mid) return query(p * 2 + 1, l, r);
    if (l <= mid && r > mid)    // 如果在左右两个子树内(合并操作)
    {
        Smtree lq = query(p * 2, l, r);     // 左子树的结果
        Smtree rq = query(p * 2 + 1, l, r); // 右子树的结果

        Smtree lca;
        pushup(lca, lq, rq);                // 计算过程父节点的值
        return lca;
    }
}

未完待续