欧拉函数

$\phi (N)$ 表示在$1 \sim N$中与$N$互质的个数

由分解质因数可得：
$$N = p_1^{\alpha_1} p_2^{\alpha_2}\dots p_k^{\alpha_k}$$

则$\phi (N)$可以表示为：
$$\phi (N) = N \times \frac{p_1 - 1}{p_1} \times \frac{p_2 - 1}{p_2}…\frac{p_k - 1}{p_k}$$

证明思路

1. 从$1 \sim N$ 中 去掉$p_1,p_2 … p_k$的所有倍数 $N - \frac{N}{p_1} - … - \frac{N}{p_k}$
2. 加上所有$p_x \times p_y$的倍数 $N - \frac{N}{p_1} - … - \frac{N}{p_k} + \frac{N}{p_1p_2} + \frac{N}{p_1p_3} + …$
3. 减去所有$p_x \times p_y \times p_x$的倍数 $N - \frac{N}{p_1} - … - \frac{N}{p_k} + \frac{N}{p_1p_2} + \frac{N}{p_1p_3} + … - \frac{N}{p_1p_2p_3} - …$
4. …

如图希望能够得到这三个集合中所有不重复元素

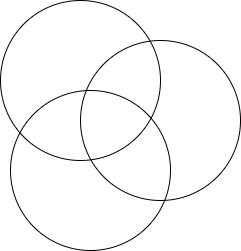
则需要先加上所有包含在单个集合中的元素，再减去重复再两个集合中的元素，再加上重复在三个集合中的元素

而将$\phi (N) = N (1 - \frac{1}{p_1})(1 - \frac{1}{p_2})…(1 - \frac{1}{p_k})$展开，则公式的每一项均可对应

使用分解质因数的模板，时间复杂度为$O(\sqrt N)$

int res = n;
for (int i = 2; i <= n / i; i++) {
    if (n % i == 0) {
        res = res / i * (i - 1); // 等价于乘上(1 - 1 / i)，变形保证不出现小数和溢出
        while (n % i == 0) n /= i;
    }
}
if (n > 1) res = res / n * (n - 1);

线性筛求欧拉函数

当求$1 \sim N$中所有数的欧拉函数，则时间复杂度为$O(N\sqrt N)$

使用线性筛可以优化到$O(N)$

1. 当i为质数时，1~i 中总共有i-1个数与其互质，即1,2,…,i-1
2. 当i为合数时
3. 当$p_j \bmod i == 0$ $p_j$为$i$的质因子 ，由于只考虑质因子的出现因此$\phi(i * p_j) = p_j\phi(i)$
4. 当$p_j \bmod i != 0$时，$p_j$小于$i$的所有质因子，$\phi(i * p_j) = p_j(1-\frac{1}{p_j})\phi(i) = (p_j-1)\phi(i)$

ph[i]表示i的欧拉函数

phi[1] = 1;
for (int i = 2; i <= n; i++) {
    if (!st[i]) {
        primes[cnt++] = i;
        phi[i] = i - 1; 
    }
    for (int j = 0; primes[j] <= n / i; j++) {
        st[primes[j] * i] = true;
        if (i % primes[j] == 0) {
            phi[primes[j] * i] = primes[j] * phi[i];
            break;
        } else
            phi[primes[j] * i] = (primes[j] - 1) * phi[i];
    }
}

欧拉定理

如果$a$与$n$互质，则$a^{\phi(n)} \bmod n = 1$

证明：

$1 \sim n$中与$n$互质的数有$\phi(n)$个，可以表示为$a_1, a_2, …, a_{\phi(n)}$

则$aa_1, aa_2, … , aa_{\phi(n)}$均与$n$互质(因为$a,a_i$均与$n$不存在相同的质因子，所以$aa_i$与$n$互质)，且两两不同，且$aa_i \bmod n < n$，所以两者相同

$$a_1a_2… a_{\phi(n)} \bmod n \equiv aa_1 aa_2 …aa_{\phi(n)} \bmod n$$
$$a^ {\phi(n)} \bmod n = 1$$

费马定理

当$n$为质数时,$a^{n-1} \bmod n = 1$

证明：

当$n$为质数时，$\phi(n) = n - 1$

$$a^ {\phi(n)} \bmod n = a^{n-1} \bmod n = 1$$

快速幂

求$a^k \bmod p$，时间复杂度为$O(\lg k)$

求解思路

使用二进制的思想，预先计算$a^{2^{0}}, a^{2^{1}}, …, a^{2^{\lg k}}$

则$a^{k} = a^{2^{i} + 2^{j} + …} = a^{2^{i}} a^{2^{j}} …$

因此使用二进制分解，将为1的位相乘即可

而在预先计算时有，$a^{2^{i}} = a^{22^{i - 1}} = (a^{2^{i - 1}})^2$，因此可以使用前一项的结果来计算当前项

static int qmi(int a, int k, int p) {
    int res = 1 % p;
    while (k > 0) {
        if ((k & 1) > 0) res = (int)((long)res * a % p); // 注意中间计算结果可能溢出，需要转化到long
        a = (int)((long)a * a % p);
        k >>= 1;
    }
    return res;
}

乘法逆元

若整数 $b, m$ 互质，并且对于任意的整数 a，如果满足 $b|a$ ，则存在一个整数 $x$，使得 $\frac{a}{b} \equiv a \times x (\bmod m)$，则称 $x$ 为 $b$ 的模 $m$ 乘法逆元，记为 $b^{−1} (\bmod m)$。
$b$ 存在乘法逆元的充要条件是 $b$ 与模数 $m$ 互质。当模数 $m$ 为质数时，$b^{m−2}$ 即为 $b$ 的乘法逆元。

即希望通过$x$使得除法转换为乘法

$\frac{a}{b} \equiv a x \Leftrightarrow \frac{a}{b} \equiv a b^{-1} \Leftrightarrow a \equiv a b b^{-a} \Leftrightarrow b b^{-1} \equiv 1$

由费马定理可知当$p$为质数时且$b,p$互质，则$b^{p-1} \equiv 1 \Leftrightarrow b b^{p-2} \equiv 1$

因为$p$为质数，因此$p-2\ge0$，所以$b^{p-2}$是$b$的一个逆元

当$b$为p的倍数时，一定有$b \times x \equiv 0 (\bmod m)$，因此不存在逆元

int p;
int res = qmi(b, p - 2, p);
if (b % p == 0) wr.write("impossible\n");
else wr.write(res + "\n");

注意不能使用res == 0进行判断，因为$p = 2$时，对于任意的$a$都有$a^{2 - 2 = 0} == 1$

扩展欧几里得算法

裴蜀定理：对于任意的正整数$a$和$b$，那么一定存在整数$x$和$y$，使得$ax+by = gcd(a, b)$

当$b = 0$时，$x = 1, y = 0$

当$b \neq 0$, 由欧几里得算法可知$(a, b) = (b, a \bmod b)$ , 不妨设$x’, y’$满足右侧等式的整数则由

$$bx’ + (a \bmod b ) y’ = (a, b)$$
$$bx’ + (a - \lfloor \frac{a}{b} \rfloor b) y’ = (a, b)$$
$$ay’ + b(x’ - \lfloor \frac{a}{b} \rfloor y’) = (a, b)$$

因此可以通过递归回溯时$x = y’, y = x’ - \lfloor \frac{a}{b} \rfloor y$，不断调整$x，y$来计算

static int x, y;
static int exgcd(int a, int b) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    } else {
        int d = exgcd(b, a % b);
        int xx = x, yy = y;
        x = yy;
        y = xx - a / b * yy;
        return d;
    }
}

注意使用xx yy临时暂存，因为x y均被进行了修改

令$d = gcd(a, b)$，则有$ax + by = d \Leftrightarrow a(x - \frac{b}{d}) + b(y + \frac{a}{d}) = d$因此在知道一组$x, y$后可以求出所有$x, y$的通项公式

$$x = x_0 - \frac{b}{d}k, y = y_0 + \frac{b}{d}k, k \in \mathbb{Z}$$

注意它包含了所有的可能解

线性同余方程

给定$a, b, m$，求$x$使其满足$a \times x \equiv b (\bmod m)$

该问题等价于$\exists y \in \mathbb{Z} st. ax = my + b$

等价变形有$ax = my + b \Leftrightarrow ax - my = b$令$y’ = -y$ 有$ax + my’ = b$

因此要保证解存在，则必须有$(a,m) | b$,此时使用扩展欧几里得算法能求出$ax + my’ = (a, m)$，等价于$ax \frac{b}{(a,m)}+ my’ \frac{b}{(a,m)} = b$

因此$x_0 \frac{b}{(a,m)}$为$a \times x \equiv b (\bmod m)$一个解，因此$x_0 \frac{b}{(a,m)} \bmod m$为该方程的一个解

int a, b, m;
int d = exgcd(a, m);
if (b % d != 0) wr.write("impossible\n");
else wr.write((long)x * b / d % m+ "\n");

中国剩余定理

给定$k$个两两互质的数$m_1,m_2, … ,m_k$,求$x$满足以下式子

$$x\equiv a_1 (\bmod m_1)$$
$$x\equiv a_2 (\bmod m_1)$$
$$…$$
$$x \equiv a_k (\bmod m_k)$$

令$M = m_1 m_2 … m_k, M_i = \frac{M}{m_i}$,令$M_iM_i^{-1} \equiv 1 (\bmod m_i)$,因此可以用扩展欧几里得算法求出该线性同余方程中的$M_i^{-1}$

则有：
$$x = a_1M_1M_1^{-1} + a_2M_2M_2^{-1} + … + a_kM_kM_k^{-1}$$

带入原式验证$\bmod m_i$有$x = a_1M_1M_1^{-1} \bmod m_i + … + a_iM_iM_i^{-1} \bmod m_i + …\Leftrightarrow x = a_1M_1M_1^{-1} \bmod m_i + … + a_i + …$，因为$M_iM_i^{-1} \equiv 1 (\bmod m_i)$

剩余项由于$M_j$中的乘积当中包含$m_i$因此$\bmod m_i = 0$，所以最终结果为$a_i$

for (int i = 0; i < n; i++) {
    M[i] = MM / m[i];
    int d = exgcd(M[i], m[i]);
    NN[i] = x * d % M[i];
}
int res = 0;
for (int i = 0; i < n; i++) {
    res += a[i] * M[i] * NN[i];
}

多线性同余方程

给定$k$个数$m_1,m_2, … ,m_k$,求$x$满足以下式子
gaigai
$$x\equiv a_1 (\bmod m_1)$$
$$x\equiv a_2 (\bmod m_1)$$
$$…$$
$$x \equiv a_k (\bmod m_k)$$

先考虑只需要满足前两个式子的简单情况$x = k_1 m_1 + a_1, x = k_2m_2 + a_2$两式联合等价于$k_1m_1 + a_1 = k_2m_2 + a_2 \Leftrightarrow k_1m_1 - k_2m_2 = a_2 - a_1$ 根据扩展欧几里得算法可知，有解等价于$(m_1, m_2) | a_2 - a_1$，则$k_1 = k_1 + k\frac{m_2}{d}, k_2 = k_2 + k\frac{m_1}{d}$

因此$x = k_1 m_1 + a_1 = (k_1 + k\frac{m_2}{d}) m_1 + a_1 = k_1 m_1 + a_1 + k \frac{m_1m_2}{d}$因此$x$的通项为$x = x_0 + km \Leftrightarrow x \bmod m = x_0$，因此可以递归地将两项式子转化为一项式子，直至将所有的式子转化为一项式子，最后一项式子有$x\equiv x_0 (\bmod m) \Leftrightarrow x = x_0 \bmod m$

long m1, a1;
long res = 0;
for (int i = 1; i  < n; i++) {
    long m2, a2;
    long d = exgcd(m1, -m2);//特别注意是-m2,求出的d可能为负数
    if ((a2 - a1) % d != 0) {
        res = -1;
        break;
    }
    long k1 = (a2 - a1) / d * x;
    k1 = (k1 % (m2/d) + (m2/d)) % (m2/d);

    a1 = k1 * m1 + a1;
    m1 = Math.abs(m1 /d * m2);
}
if (res != -1) {
    res = (a1 % m1 + m1) % m1;
}

不定方程

对于不定方程$x = x_0 + kt$ 或$x \equiv x_0 (\bmod t)$，求满足方程最小非负整数$x$

由于要使得数尽可能地小，因此当$x_0 > 0$， x = x_0 % t当$x_0 \leq 0$，x = x_0 % t + t。因此统一结果为x = (x_0 % t + t) % t