搜索

树的基本操作

树的深度

d[0] = 0;           // 根节点深度为 0
d[j] = d[i] + 1;    // i 是 j 的父节点

示例程序：

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) 
        {
            d[j] = d[i] + 1; // 深度更新
            dfs(j);
        }
    }
}

树的大小

求出 每一个子树 的 节点数

int dfs(int u)
{
    size[u] = 1;
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) 
        {
            dfs(j);
            size[i] += size[j];
        }
    }
}

1.深度优先搜索

深度优先搜索的要点

1. 有调用的 终止条件

2. 回溯时 需要 还原现场

3. 先确定 问题空间的状态, 如 小猫爬山 中的两种状态 （now, cnt) 分别表示 (当前装到第几只猫，所用缆车数）

4. 画图有助于我们 更好的理解递归问题

1. 图的深搜

标记 已经遍历过边 的点，并搜索 未被遍历 过的所有节点。

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

2.树的 DFS 序列

特点 ： 每个节点均会在 DFS序列中出现两次，分别是 进入 和 离开 DFS序列的时候。

void dfs(int u)
{
    a[ ++ m] = x; // a 数组储存 DFS序列
    st[u] = true;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i] // e 是当前遍历到的节点
        if (!st[j])
        {
            dfs(j);
        }
    }
    a[++ m] = x;
}

给一张图，便于理解：

3. 剪枝

为了方便读者阅读，我先把搜索树挂上：

1、可行性剪枝

所谓可行性剪枝，顾名思义，就是当当前状态和题意不符，并且由于题目可以推出，往后的所有情况和题意都不符，那么就可以进行剪枝，直接把这种情况及后续的所有情况判负，直接返回。

即：不可行，就返回。

2、排除等效冗余

所谓排除等效冗余，就是当几个枝丫具有 完全相同的效果 的时候，只选择其中一个走就可以了。

即：都可以，选一个。

3、最优性剪枝

所谓最优性剪枝，是在我们用搜索方法解决最优化问题的时候的一种常用剪枝。就是当你搜到一半的时候，已经比 搜到的最优解要不优了，那么这个方案肯定是不行的，即刻停止搜索，进行回溯。

即：有比较，选最优。

4、顺序剪枝

普遍来讲，搜索的顺序是不固定的，对一个问题来讲，算法可以进入搜索树的任意的一个子节点。但假如我们要搜索一个最小值，而非要从最大值存在的那个节点开搜，就可能存在搜索到最后才出解。而我们从最小的节点开搜很可能马上就出解。这就是顺序剪枝的一个应用。一般来讲，有单调性存在的搜索问题可以和贪心思想结合，进行顺序剪枝。

即：有顺序，按题意。

5、记忆化

记忆化搜索其实是搜索的另外一个分支。在这里简单介绍一下记忆化的原理：

就是记录搜索的每一个状态，当 重复搜索到相同的状态 的时候直接返回。

即：搜重了，直接跳。

4. 迭代加深

使用条件 ： 确保在较浅的子树上可以搜到，列如，出现：” 十步之内得出答案的 “ 就直接用了。

概念

迭代加深（Iterative deepening）搜索，实质上就是限定下界的深度优先搜索。即首先允许深度优先搜索K层搜索树，若没有发现可行解，再将K+1后重复以上步骤搜索，直到搜索到可行解。

在迭代加深搜索的算法中，连续的深度优先搜索被引入，每一个深度约束逐次加1，直到搜索到目标为止。

迭代加深搜索算法就是仿广度优先搜索的深度优先搜索。既能满足深度优先搜索的线性存储要求，又能保证发现一个最小深度的目标结点。

从实际应用来看，迭代加深搜索的效果比较好，并不比广度优先搜索慢很多，但是空间复杂度却与深度优先搜索相同，比广度优先搜索小很多，在一些层次遍历的题目中，迭代加深不失为一种好方法！

代码示例

bool dfs(int u)
{
    if (u == depth) return;
    ...
        return false;
}

int main()
{
    while(!dfs(0)) depth ++;
}

双向搜索

我们常常会面临这样一类搜索问题：起点是给出的，终点也是已知的，需要确定能否从起点到达终点，如果可以，需要多少步。

比如这样

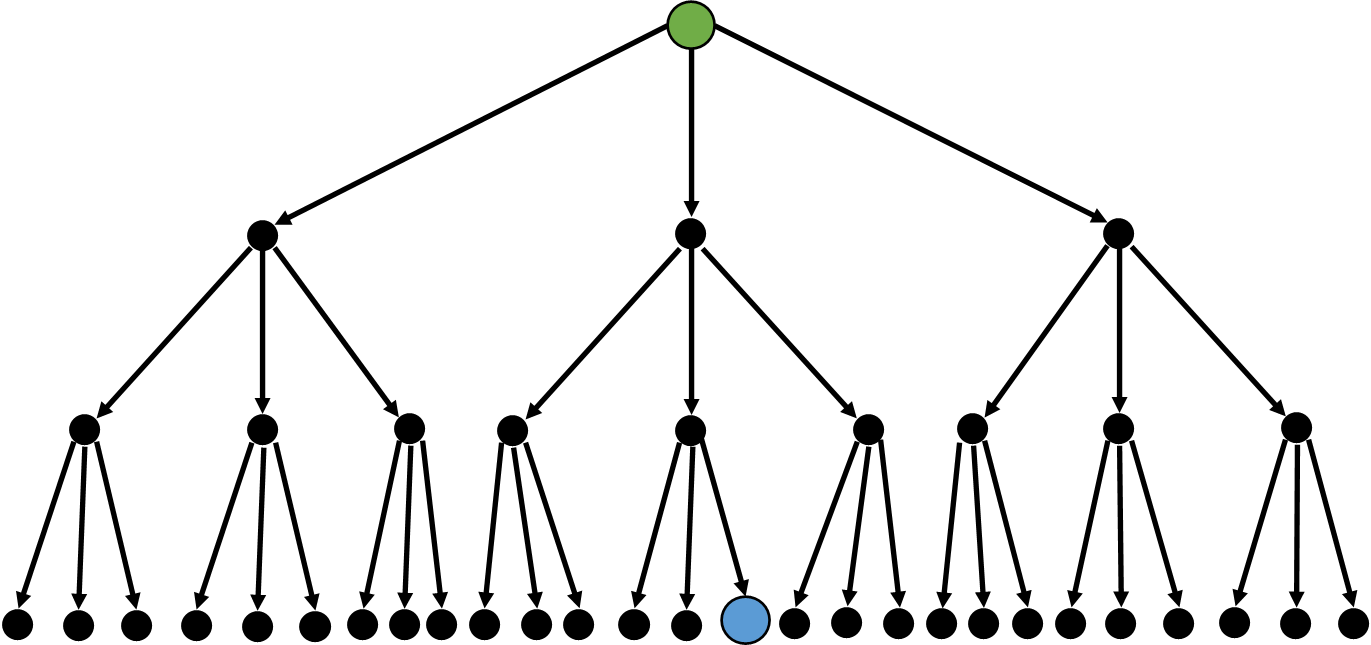
那怎么样才能简化这个问题呢？

其实我们完全可以分别从 起点和 终点 出发，看它们能否 相遇

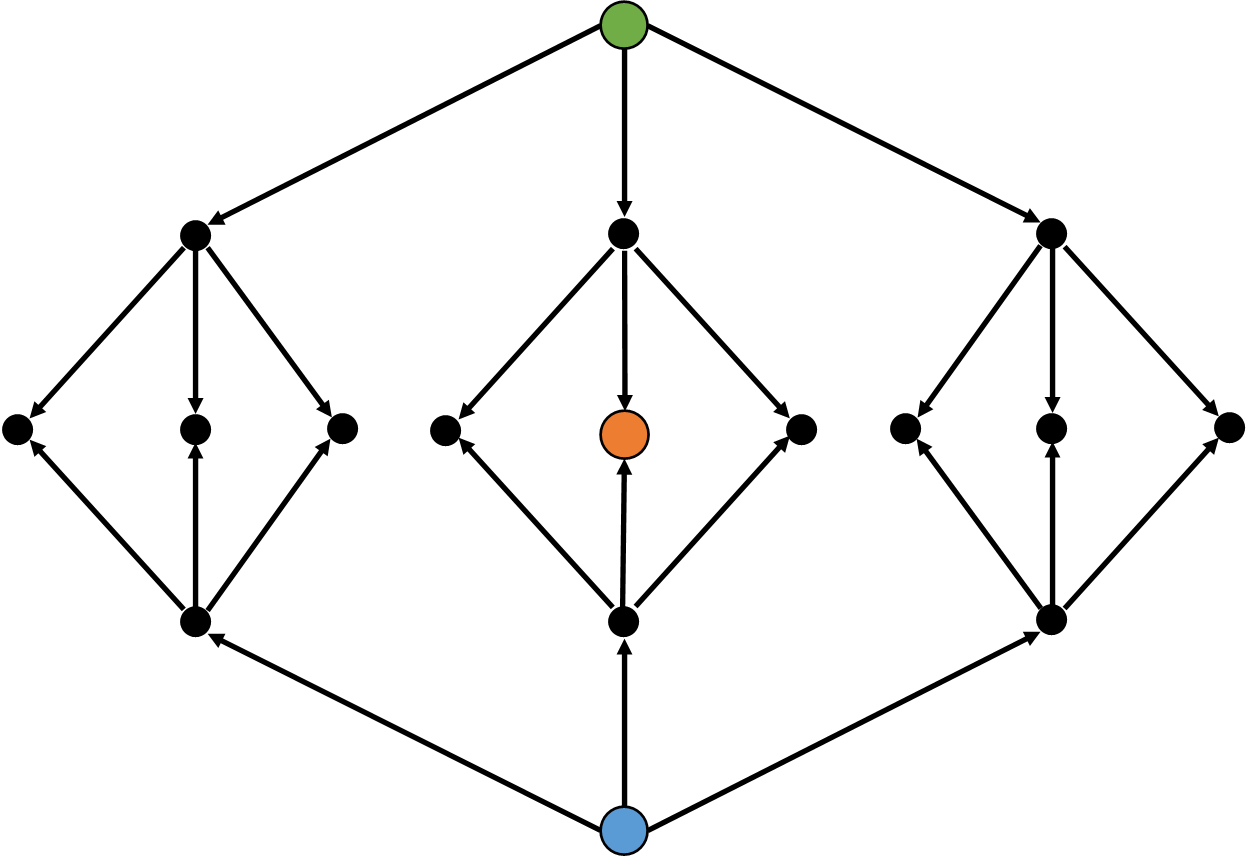
这，就是双向搜索~

双向搜索主要有两种，双向BFS和双向迭代加深。

双向BFS

与普通的 BFS 不同，双向 BFS 维护 两个 而不是 一个 队列，

然后轮流 拓展两个队列。同时，用数组（如果状态可以被表示为较小的整数）或哈希表 记录当前的搜索情况，给从两个方向 拓展的节点 以不同的标记。

当某点被两种标记 同时标记时，搜索结束。

queue<T> Q[3]; // T要替换为用来表示状态的类型，可能为int，string还有bitset等
bool found = false;
Q[1].push(st); // st为起始状态
Q[2].push(ed); // ed为终止状态
for (int d = 0; d < D + 2; ++d) // D为最大深度，最后答案为d-1
{
    int dir = (d & 1) + 1, sz = Q[dir].size(); // 记录一下当前的搜索方向，1为正向，2为反向
    for (int i = 0; i < sz; ++i)
    {
        auto x = Q[dir].front();
        Q[dir].pop();
        if (H[x] + dir == 3) // H是数组或哈希表，若H[x]+dir==3说明两个方向都搜到过这个点
            found = true;
        H[x] = dir;
        // 这里需要把当前状态能够转移到的新状态压入队列
    }
    if (found)
        // ...
}

例题 AcWing 177 噩梦

双向迭代加深

双向迭代加深就是相应地，从两个方向迭代加深搜索。

先从起点开始搜 0层，再从终点开始搜 0层，然后从起点开始搜 1层……

int D;
bool found;
template <class T>
void dfs(T x, int d, int dir)
{
    if (H[x] + dir == 3)
        found = true;
    H[x] = dir;
    if (d == D)
        return;
    // 这里需要递归搜索当前状态能够转移到的新状态
}

// 在main函数中...
while (D <= MAXD / 2) // MAXD为题中要求的最大深度
{
    dfs(st, 0, 1); // st为起始状态
    if (found)
        // ...
        // 题中所给最大深度为奇数时这里要判断一下
    dfs(ed, 0, 2); // ed为终止状态
    if (found)
        // ...
    D++;
}

广度优先搜索

先放个图

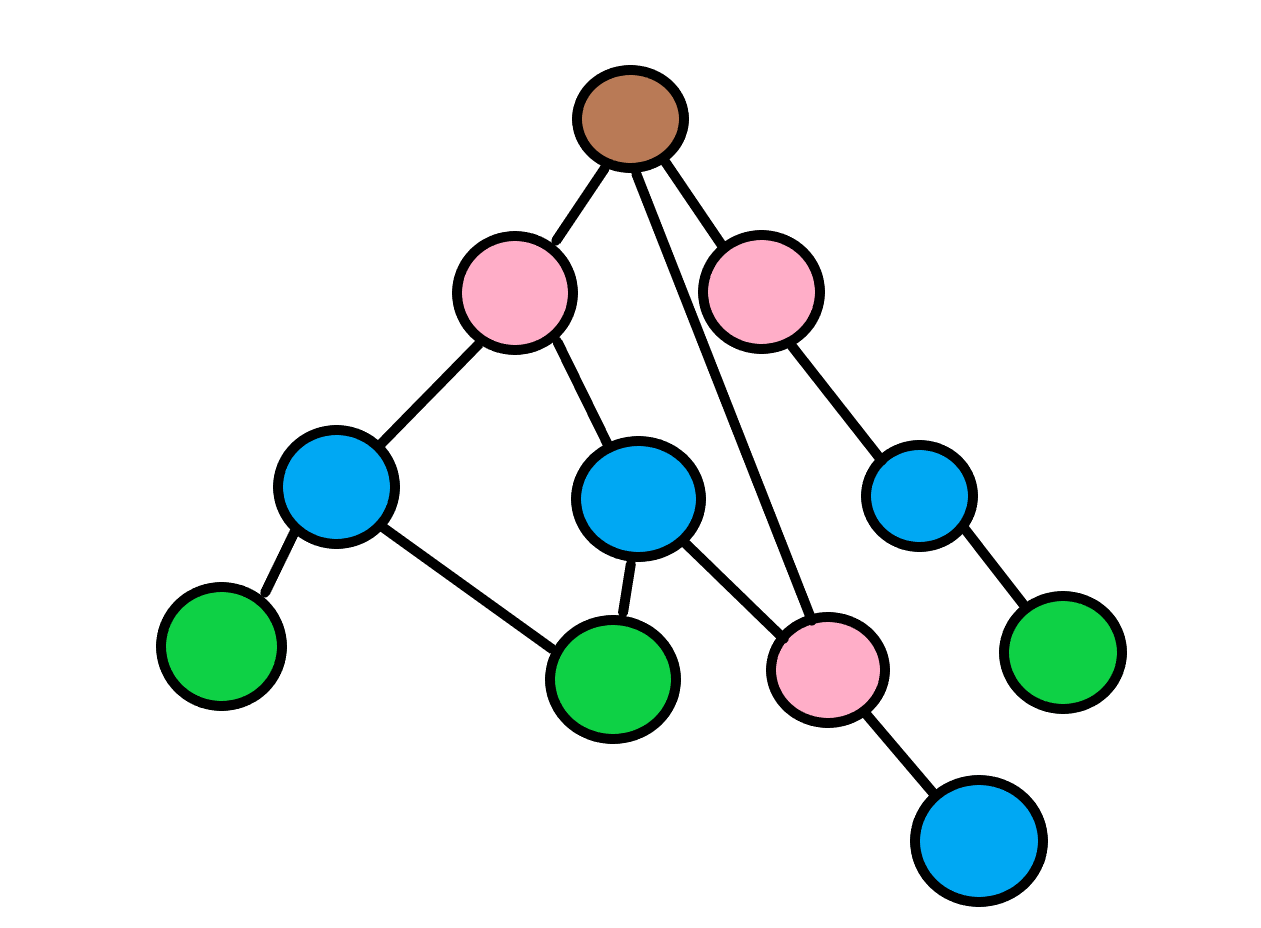
用 队列 实现

不断从队头取出状态， 把 每条出边 遍历，未被遍历过 的节点就 更新距离 并 加入队尾，直到队列 为空。

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

下面这个动图就是用 BFS 实现的

双端队列 BFS

用 双端队列 实现

解决边权为 1 或 0 的图时， 将 边权为 0 的状态 压入 队头，边权为 1 的 压入 队尾，这样就可以 优先 更新边权为 0 的状态了！

最小步数模型

比如说这道题 AcWing 1107. 魔板 问你从 一种状态 到 另外一种状态 要通过多少步，

通常，我们遇到这种题的时候，要注意怎样才能将它的 所有状态， 储存 或 映射 下来，

因为每一个操作的步数是相等的，所以 第一个 与最终状态 相等的状态 所用的步数，就是 最短步数

方案

可以通过储存到达每一个点时上一步的状态，最后，从终点出发，逆序返回起点，倒着输出就是方案数了。

因为 $BFS$ 的每一个状态或点只经过一次，所以可以确保这么做是正确的。

AcWing 1076. 迷宫问题

拓扑排序

有向图 才有拓扑排序

将 入度 为 0 的点入队，并遍历其所有出边，将所有
出边上的点 入度 - 1 若 入度为 0 便 入队，按上述操作 遍历，直到 队列为空

时间复杂度 $O(n + m)$

bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i; // q.push(i);

    while (hh <= tt)
    {
        int t = q[hh ++ ]; // q.front(), q.pop();

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j; // q.push(j);
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}

有些时候，也有用 邻接矩阵 实现的。

A* 算法

在最短路问题中，如果所有边权非负，就可以用 A*算法 优化 最短路算法