题目描述
平面上有 N 条直线,其中第 i 条直线是 y=Ai⋅x+Bi。
请计算这些直线将平面分成了几个部分。
输入格式
第一行包含一个整数 N。
以下 N 行,每行包含两个整数 Ai,Bi。
输出格式
一个整数代表答案。
数据范围
对于 50% 的评测用例,1≤N≤4,−10≤Ai,Bi≤10。
对于所有评测用例,1≤N≤1000,−100000≤Ai,Bi≤100000。
样例
输入样例:
3
1 1
2 2
3 3
输出样例:
6


两条直线交点的坐标
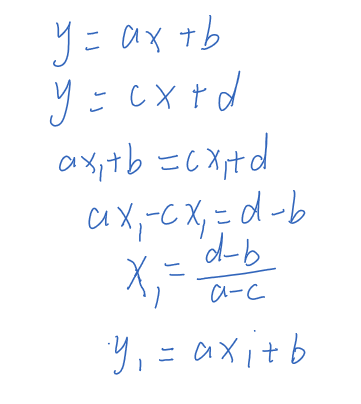
set容器的元素访问
注意如果使用set[HTML_REMOVED]> s,只能采用auto t=s->first,不能用.访问
// 注意如果使用set<pair<int,int>> s,只能采用auto t=s->first,不能用.访问
#include<iostream>
#include<set>
using namespace std;
int main()
{
set<int>st;
st.insert(3);
st.insert(5);
st.insert(5);
st.insert(2);
for(auto it=st.begin();it!=st.end();it++)
cout<<*it<<" ";
return 0;
}
C++ 代码
#include<iostream>
#include<set>//set为集合可以自动去重
using namespace std;
/*
1、重边不会影响区域数目。
2、每新加入一条边只要不是重边区域数目必定+1。
3、加入的新边如果与之前加入的边每有一个交点则区域数目+1。
*/
typedef pair<double,double> pdd;//存放A和B
set<pdd> lines;//存放直线因为可以去重,重边无贡献
int res=1; // 这里注意要从1开始,因为本就有一个部分
int cmp(double c,double d){//求此条直线与之前所有直线的交点个数
set<pdd> points;//交点的集合
pdd it;//交点
for(auto i=lines.begin();i!=lines.end();i++){
double a=i->first,b=i->second;
if(a!=c){//斜率不同则两条直线不重合
it.first=(d-b)/(a-c);//求交点的横坐标
it.second=c*it.first+d; //使用a和b求不通过??
points.insert(it);
}
}
return points.size();
}
int main(){
int n;
cin>>n;
while(n--){
double a,b;
cin>>a>>b;
int count1=lines.size();//count1为未加入现在这条边的总的边数
lines.insert({a,b});//将输入的x和y保存到line中
//如果现在加入的边是重边则无影响下面的if语句不会执行,如果不是重边则count1就不会等于增加后的边数
if(lines.size()!=count1){
res++;
res+=cmp(a,b);
}
}
cout<<res<<endl;
return 0;
}


纵坐标不用直接代入,消掉x保留y就可以过
double y=(a1b2-a2b1)/(a1-a2);
佬为什么 要用都double来存储pdd啊,用int的话就只能过两个点
借用一下佬的这篇题解,来写笔记,补题
感谢大佬,ac了
巨佬,我也发现使用a,b只能过7个数据,您知道原因吗?
感觉应该和double的精度有关系,和2021的直线那题一样,当小于esp(1e-8)时就应当认为是同一个值
我写了一个可以解决精度问题的,由于set的迭代器不会自己写,所以用了一个数组来保存.
牛掰
很不错的题解