题目描述

给定 n 个正整数 ai，请你求出每个数的欧拉函数。

欧拉函数的定义
1∼N 中与 N 互质的数的个数被称为欧拉函数，记为 ϕ(N)。
若在算数基本定理中，N=pa11pa22…pamm，则：
ϕ(N) = N×p1−1p1×p2−1p2×…×pm−1pm
输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
输出共 n 行，每行输出一个正整数 ai 的欧拉函数。

数据范围
1≤n≤100,
1≤ai≤2×109

样例

输入样例：
3
3
6
8
输出样例：
2
2
4

算法1

欧拉函数：给定一个数n，返回与n互质的数的个数。(互质：与n的最大公因数是1)
题目给出了欧拉函数的公式，按照公式求解不难，主要是要理解公式的原理。
公式证明


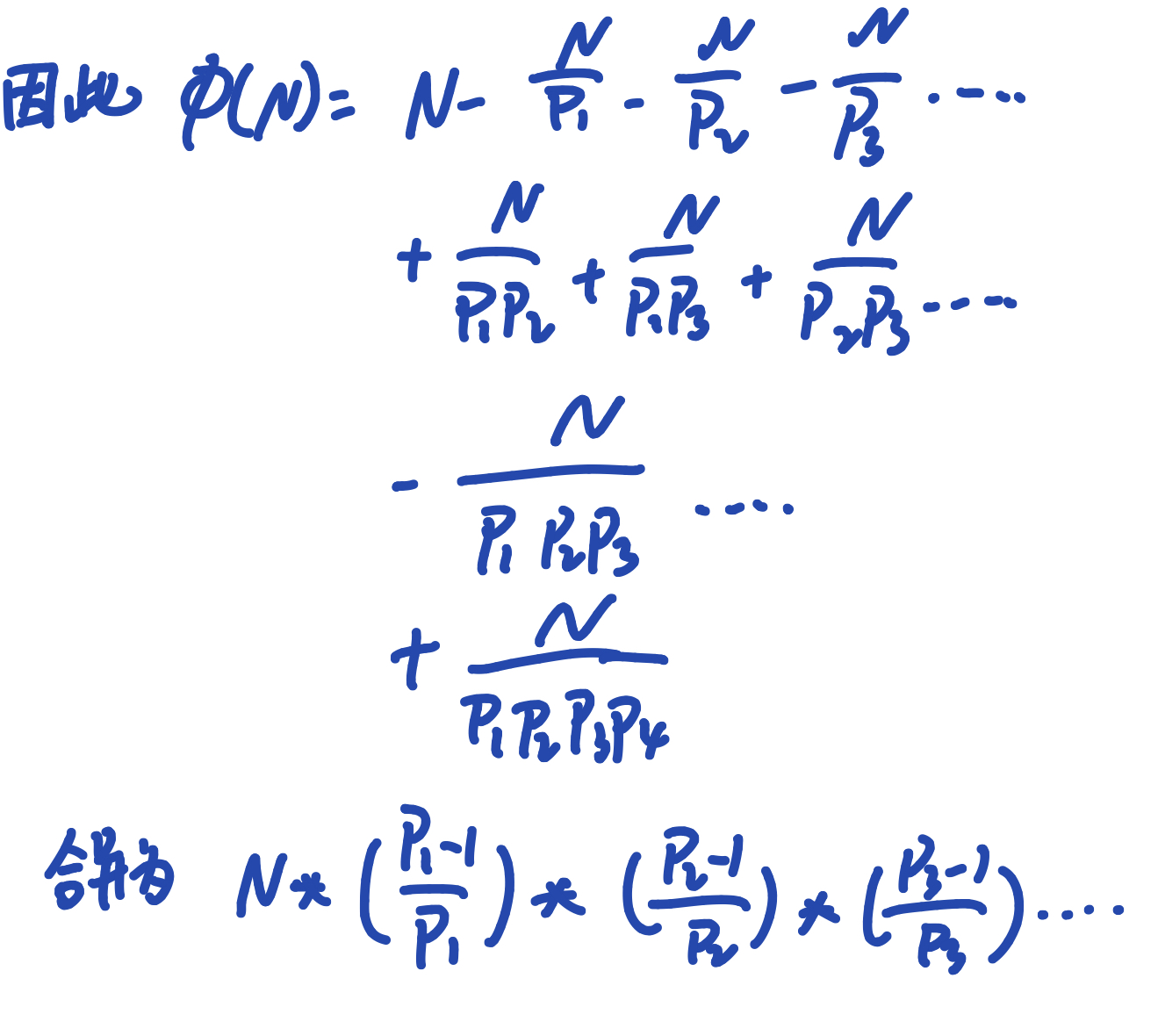
代码部分要注意
在进行N*(p-1)/p时，由于是先算的乘法，可能乘法的结果超过了int的范围，也就是爆精度，因此要先做除法，然后再做乘法

result = result/p*(p-1);

C++ 代码

#include <iostream>
#include <vector>
using namespace std;

int Euler(int x){
    int result = x;
    vector<int> prime;
    for(int i = 2;i<=x/i;i++){
        if(x%i==0){
            prime.push_back(i);
            while(x%i==0){
                x/=i;
            }
        }
    }
    if(x>1)prime.push_back(x);
    for(auto p:prime){
        result = result/p*(p-1);
    }
    return result;
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        cout<<Euler(x)<<endl;
    }
}