单词接龙是一个与我们经常玩的成语接龙相类似的游戏。

现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”，每个单词最多被使用两次。

在两个单词相连时，其重合部分合为一部分，例如 beast 和 astonish ，如果接成一条龙则变为 beastonish。

我们可以任意选择重合部分的长度，但其长度必须大于等于1，且严格小于两个串的长度，例如 at 和 atide 间不能相连。

输入格式
输入的第一行为一个单独的整数 nn 表示单词数，以下 nn 行每行有一个单词（只含有大写或小写字母，长度不超过20），输入的最后一行为一个单个字符，表示“龙”开头的字母。

你可以假定以此字母开头的“龙”一定存在。

输出格式

只需输出以此字母开头的最长的“龙”的长度。

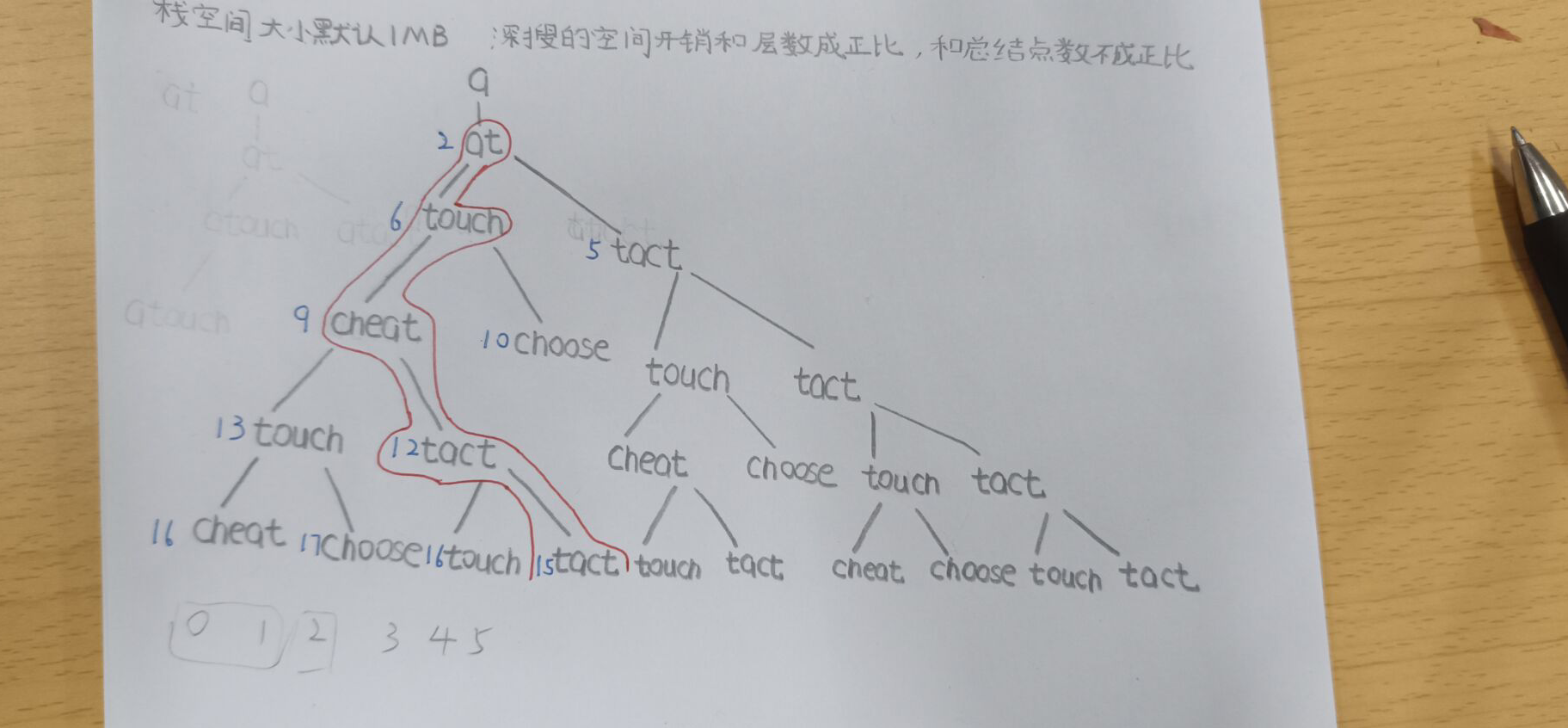
最重要的应该是想到把问题转化成决策树（当满足条件代表两个字符串可以连一条边）

数据范围

n≤20n≤20，
单词随机生成。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 21;

string word[N];
int used[N], g[N][N];
int n, ans;

void dfs(string dragon, int last)
{
    ans = max(ans, (int)dragon.size());

    used[last] ++;

    for(int i = 0; i < n; i++)
     if(g[last][i] && used[i] < 2) 
      dfs(dragon + word[i].substr(g[last][i]), i);

    used[last] --;
}
int main()
{
    cin >> n;
    for(int i = 0; i < n; i++) cin >> word[i];
    char start;
    cin >> start;

    for(int i = 0; i < n; i++)
     for(int j = 0; j < n; j++)
      {
          string a = word[i], b = word[j];
          for(int k = 1; k < min(a.size(), b.size()); k++)
           if(a.substr(a.size() - k, k) == b.substr(0, k)) {g[i][j] = k;break;}  // 重合长度越小单词能接的龙长度越大
      }

    for(int i =0; i < n; i++)
     if(word[i][0] == start) dfs(word[i], i);

    cout << ans << endl;

    return 0;
}