画了个图，理解左右子树的起点和终点位置

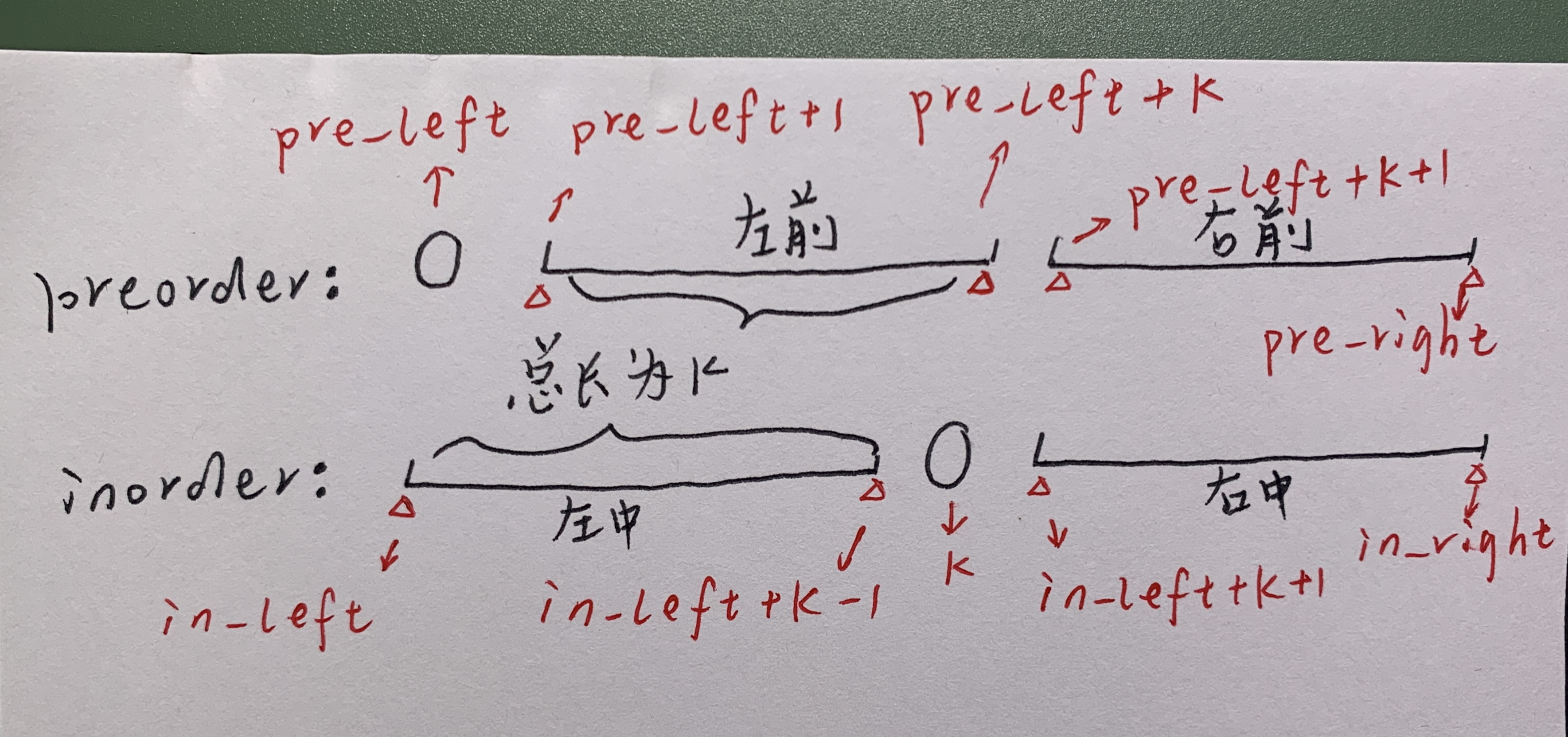
根在中序遍历中的相对位置为 k
左中序列(in_left, in_left + k - 1), 左前序列(pre_left + 1, pre_left + k),
右中序列(in_left + k + 1, in_right), 右前序列(pre_left + k + 1, pre_right)

class Solution {
public:
    // 记录每个结点在中序遍历序列中的位置
    unordered_map<int, int> pos;

    // DFS递归遍历二叉树
    TreeNode* dfs(vector<int>& pre, vector<int>& in, 
        int pre_left, int pre_right, int in_left, int in_right) {

        // 递归结束条件
        if (pre_left > pre_right) return NULL;

        // 当前根结点 为先序遍历的第一个结点
        TreeNode* root = new TreeNode(pre[pre_left]);

        // k 表示根在中序遍历中的相对位置
        int k = pos[root->val] - in_left;

        root->left = dfs(pre, in, pre_left + 1, pre_left + k, in_left, in_left + k - 1);
        root->right = dfs(pre, in, pre_left + k + 1, pre_right, in_left + k + 1, in_right);

        return root;
    }

    // 根据前序遍历和中序遍历，构建二叉树
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {

        // 记录每个结点在中序遍历序列中的位置
        int n = inorder.size();
        for (int i = 0; i < n; i++) pos[inorder[i]] = i;

        return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
    }
};