阿巴阿巴
0x01 位运算
AcWing89.a^b
快速幂模板题。
令 $k$ 为 $b$ 在二进制下的位数,$t_i$ 为 $b$ 在二进制下的第 $i$ 位。
则 $b = t_{k - 1} {2^{k - 1}} + t_{k - 2} 2 ^ {k - 2} + … + t_02_0$
于是 $a ^ b = a^{t_{k - 1}{2^{k - 1}}} * a^{t_{k - 2}{2^{k - 2}}} * … * a^{t_02_0}$
所以我们只要将 $b$ 二进制中所有为 $1$ 的位 $i$,取出,答案即为所有 $a^{t_{i}2_i}$ 的乘积。
#include <iostream>
using namespace std;
typedef long long LL;
LL a, b, p;
int main() {
scanf("%lld%lld%lld", &a, &b, &p);
LL res = 1 % p;
while (b) {
if (b & 1) res = res * a % p;
b >>= 1;
a = a * a % p;
}
printf("%lld\n", res);
return 0;
}
AcWing90. 64位整数乘法
思路类似快速幂。
令 $b = t_{k - 1} {2^{k - 1}} + t_{k - 2} 2 ^ {k - 2} + … + t_02_0$
则 $a * b = a \times t_{k - 1}{2^{k - 1}} + a \times t_{k - 2}{2^{k - 2} + … + a \times t_02_0}$
同样地,我们可以枚举每一个为 $1$ 的二进制位,然后通过以上式子进行计算。
#include <iostream>
using namespace std;
typedef long long LL;
LL a, b, p;
int main() {
cin >> a >> b >> p;
LL res = 0;
while (b) {
if (b & 1) res = (res + a) % p;
b >>= 1;
a = (a + a) % p;
}
cout << res << endl;
return 0;
}
AcWing998. 起床困难综合症
由于给出的二进制运算的特点是不进位,所以每一位的计算是独立的。由于题目要求我们求出经过 $n$ 次操作后答案最大的 $x$ 并且 $x \in [0,m]$,所以可以从高位到低位分别枚举 $x$ 的每一位上填 $0$ 还是填 $1$。
具体的,$x$ 的第 $i$ 位可以填 $1$ 当且仅当:
1. 填上 $1$ 后 $x <= m$
2. 该位填 $1$ 优于该位填 $0$
首先第一种情况,我们只要判断当前 $x + (1 << i)$ 是否小于 $m$;
第二种情况,我们分别计算填 $1$ 和 填 $0$ 后的答案,比较即可确定该位的填法。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m, ans;
int t[N], op[N];
int work(int x, int j) {
for (int i = 1; i <= n; i ++) {
if (op[i] == 1) x &= t[i] >> j & 1;
else if (op[i] == 2) x |= t[i] >> j & 1;
else x ^= t[i] >> j & 1;
}
return x;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) {
char s[10];
scanf("%s %d", s, &t[i]);
if (*s == 'A') op[i] = 1;
else if (*s == 'O') op[i] = 2;
else op[i] = 3;
}
for (int i = 30; i >= 0; i --) {
if (1 << i <= m) {
int x = work(0, i), y = work(1, i);
if (x >= y) ans |= x << i;
else ans |= y << i, m -= 1 << i; // 这里填 1 时直接用m减掉 1 << i,方便判断
} else {
ans |= work(0, i) << i;
}
}
printf("%d\n", ans);
return 0;
}
AcWing91. 最短Hamilton路径
状压 DP 入门题。
状态表示($f_{i,j}$)
- 集合:当前经过点的状态为 $i$,最后停在了 $j$ 上。其中若 $i$ 二进制的第 $k$ 位为 $1$ 则表示已经经过了第 $k$ 个点,反之亦然。
- 属性:$\min$
状态计算:考虑我们上一步是从 $k$ 来到 $j$ 的,那么我们的状态转移方程就应该是
$$f_{i,j} = \min{f_{i,j}, f_{i - 2 ^ j, k} + w_{k, j}}$$
初始化:$f_{1, 0} = 0$,其余均为 $INF$
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 21, M = 1 << 21;
int n;
int f[M][N], w[N][N];
int main() {
cin >> n;
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++)
cin >> w[i][j];
memset(f, 0x3f, sizeof f);
f[1][0] = 0;
for (int i = 0; i < 1 << n; i ++)
for (int j = 0; j < n; j ++)
if (i >> j & 1)
for (int k = 0; k < n; k ++)
if (i >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][n - 1];
return 0;
}
0x02 递推与递归
AcWing 95. 费解的开关
我们可以发现几个性质:
1. 我们点灯的先后顺序不影响结果。
2. 一个位置至多被点击一次
3. 如果我们将第一行固定,那么想改变第一行就有且只有一种可能,便是操作该灯下方第二行的灯。
结合以上性质,我们可以进行递推,先固定第一行,然后操作第二行,接着再操作第三行,最后我们只要判断第五行操作完后是否为 $1$ 即可。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int n;
char g[5][5], backup[5][5];
void turn(int x, int y) {
int dx[5] = {-1, 0, 0, 0, 1}, dy[5] = {0, -1, 0, 1, 0};
for (int i = 0; i < 5; i ++) {
int xx = x + dx[i], yy = y + dy[i];
if (xx >= 0 && xx < 5 && yy >= 0 && yy < 5)
g[xx][yy] ^= 1;
}
}
void solve() {
int ans = 0x3f3f3f3f;
for (int k = 0; k < 1 << 5; k ++) {
int res = 0;
memcpy(backup, g, sizeof g);
for (int i = 0; i < 5; i ++)
if (k >> i & 1) {
res ++;
turn(0, i);
}
for (int i = 0; i < 4; i ++)
for (int j = 0; j < 5; j ++)
if (g[i][j] == '0') {
res ++;
turn(i + 1, j);
}
bool ok = true;
for (int i = 0; i < 5; i ++)
if (g[4][i] == '0')
ok = false;
if (ok) ans = min(ans, res);
memcpy(g, backup, sizeof backup);
}
if (ans > 6) ans = -1;
printf("%d\n", ans);
}
int main() {
int T; scanf("%d", &T);
while (T --) {
for (int i = 0; i < 5; i ++) scanf("%s", g[i]);
solve();
}
return 0;
}
AcWing 96. 奇怪的汉诺塔
考虑 $n$ 盘 $3$ 塔的汉诺塔问题,令 $d_i$ 表示 $i$ 盘 $3$ 塔问题的步数。我们考虑先将 $i - 1$ 个盘子从 $A$ 柱放到 $B$ 柱,再把剩下的一个盘子放到 $C$ 柱,最后再把 $B$ 柱上的 $i - 1$ 个盘子放到 $C$ 柱上。
通过以上步骤,可以写出递推式 $d_i = 2 \times d_{i - 1} + 1$
接着考虑 $4$ 塔问题。令 $f_i$ 表示 $i$ 盘 $4$ 塔问题的步数。
我们可以先将 $j$ 个盘子从 $A$ 移到 $B$,剩下的 $n - j$ 个盘子做 $3$ 塔问题,从 $A$ 移到 $D$,最后再把 $B$ 柱上的 $j$ 个盘子做 $4$ 塔问题,移到 $D$ 上。
类似的,我们可以写出递推式 $f_i = \underset{1 \leq j < i}\min(2 \times f_{j} + d_{n - j})$
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 15;
int n, f[N], d[N];
int main() {
scanf("%d", &n);
memset(f, 0x3f, sizeof f);
f[1] = 1, d[1] = 1;
for (int i = 2; i <= 12; i ++)
for (int j = 1; j < i; j ++) {
f[i] = min(f[i], 2 * f[j] + d[i - j]);
d[i] = 2 * d[i - 1] + 1;
}
for (int i = 1; i <= 12; i ++)
cout << f[i] << endl;
return 0;
}
AcWing97. 约数之和
令 $A = p_1^{k_1}\times p_2^{k_2}\times … \times p_n^{k_n} $
那么 $A^B = p_1^{k_1B}\times p_2^{k_2B}\times … \times p_n^{k_nB}$
由约数之和的公式可得,$A^B$ 的约数之和为 $(1 + p_1 + p_1^{2} + … + p_1^{k_1B}) \times … \times (1 + p_n + p_n ^ 2 + … + p_n ^ {k_nB})$
暴力循环计算以上式子肯定会超时,所以我们可以采用分治的思想。
我们考虑如何快速计算 $1 + p + p ^ 2 + … + p ^ n$。
首先,我们令 $1 + p + p ^ 2 + … + p ^ n = S(p, n)$
接着我们根据 $n$ 的奇偶性分两类讨论:
-
$n$ 为奇数
$ S(p,n) = (1 + p + … + p ^ {\frac{n - 1}{2}}) + (p ^ {\frac{n + 1}{2}} + … + p ^ n) $
$=(1 + p + … + p^{\frac{n - 1}{2}}) + p ^ {\frac{n + 1}{2}}(1 + p + … + p^{\frac{n-1}{2}})$
$=(1 + p^{\frac{n+1}{2}})(1 + p + … + p^{\frac{n - 1}{2}})$
$=(1 + p^{\frac{n+1}{2}})\times S(p, \frac{n - 1}{2})$
-
$n$ 为偶数
$ S(p,n) = (1 + p + … + p^{\frac{n}{2} - 1}) + (p^{\frac{n}{2}} + … + p^n)$
$= (1 + p + … + p^{\frac{n}{2} - 1}) + p^{\frac{n}{2}}(1 + … + p ^ {\frac{n}{2}})$
$= (1 + p + … + p^{\frac{n}{2} - 1}) + p^{\frac{n}{2}}(1 + … + p ^ {\frac{n}{2} - 1}) + p^n$
$= (p^{\frac{n}{2}} + 1)\times S(p, \frac{n}{2} - 1) + p^n$
由此,我们便用 $O(logn)$ 的时间计算出 $S(p,n)$、
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int Mod = 9901;
typedef long long LL;
int a, b;
LL qmi(int a, int b) {
a %= Mod;
LL res = 1;
while (b) {
if (b & 1) res = res * a % Mod;
b >>= 1;
a = a * a % Mod;
}
return res;
}
LL work(int p, int n) {
if (n == 0) return 1;
if (n & 1) return (qmi(p, n + 1 >> 1) + 1) * work(p, n - 1 >> 1) % Mod;
else return ((qmi(p, n >> 1) + 1) * work(p, (n >> 1) - 1) % Mod + qmi(p, n)) % Mod;
}
int main() {
scanf("%d%d", &a, &b);
LL res = 1;
for (int i = 2; i <= a / i; i ++) {
int cnt = 0;
while (a % i == 0) a /= i, cnt ++;
res = res * work(i, cnt * b) % Mod;
}
if (a > 1) res = res * work(a, b) % Mod;
if (a == 0) res = 0;
printf("%lld\n", res);
return 0;
}
0x03 前缀和与差分
AcWing99. 激光炸弹
二维前缀和应用题。
枚举被炸区域的右下角,然后用二维前缀和计算 $(i - r + 1, j - r + 1)$ ~ $(i, j)$ 的总和,取最大值即可。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010, M = 5010;
int n, r;
int g[M][M], s[M][M];
int main() {
scanf("%d%d", &n, &r);
for (int i = 1; i <= n; i ++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
s[x + 1][y + 1] += z;
}
int ans = -1;
r = min(r, 5001);
for (int i = 1; i <= 5001; i ++)
for (int j = 1; j <= 5001; j ++)
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
for (int i = r; i <= 5001; i ++)
for (int j = r; j <= 5001; j ++)
ans = max(ans, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);
printf("%d\n", ans);
return 0;
}
AcWing100. 增减序列
观察题目,我们每次操作只会对某个区间加或减 $1$,所以我们可以使用差分。
令 $b$ 为 $a$ 的差分数组,即 $b_i = a_i - a_{i - 1}$,这样对区间 $[l,r]$ 进行修改时只需要分别修改 $b_l$ 和 $b_{r + 1}$ 即可。
因为要使 $a$ 中的所有数都一样,所以 $b_2$ ~ $b_n$ 必须等于 $0$,而 $b_1$ 可以为任意数。
接下来考虑操作,一共四种情况:
1. 选择 $b_1$ 和 $b_{n+1}$
2. 选择 $b_1$ 和 $b_{j}(j \leq n)$
3. 选择 $b_j(j > 1)$ 和 $b_{n+1}$
4. 选择 $b_i$ 和 $b_{j}$,其中 $2\leq i,j\leq n$
第一种情况无意义不考虑,剩下三种情况中,如果 $b$ 中同时存在正数和负数,我们应该优先考虑第四种情况,然后才是考虑第二种情况和第三种情况。
所以我们设 $b_2, b_3, …, b_n$ 中有 $p$ 个整数,$q$ 个负数,那么最小操作次数就应该是 $\min(p, q) + |p - q| = \max(p, q)$。
而在 $|p - q|$ 次的操作过程中,我们可以选择第二种操作也可以选择第三种操作,所以可能得到的结果(也就是 $b_1$ 的值)会有 $|p - q| + 1$ 种。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
long long n, a[N], b[N];
long long p, q;
int main() {
scanf("%lld", &n);
for (int i = 1; i <= n; i ++) {
scanf("%lld", &a[i]);
b[i] = a[i] - a[i - 1];
}
for (int i = 2; i <= n; i ++)
if (b[i] > 0) p += b[i];
else q -= b[i];
printf("%lld\n%lld\n", max(p, q), abs(p - q) + 1);
return 0;
}
AcWing101. 最高的牛
注意到如果 $a < b < c < d$,且$a$ 和 $c$ 可以互相看到的话,$b$ 和 $d$ 一定无法互相看到。
于是我们便可以用差分维护这个关系。具体的,如果 $l$ 和 $r$ 可以互相看到的话,就让差分数组 $b$ (初始都为 $0$) 中的 $b_{l + 1} -1, b_{r} +1$,这样 $l$ 和 $r$ 之间的牛的高度都会下降 $1$。然后对 $b$ 求前缀和,求完后再给前缀和数组中的每一头牛的高度都加上 $H$,也就是最高的牛的身高。
这种思想为 把对一个区间的操作转化成左右两端上的操作,再通过前缀和得到原问题的解。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
const int N = 5010;
int n, p, h, m;
int b[N];
map<pair<int, int>, bool> H;
int main() {
scanf("%d%d%d%d", &n, &p, &h, &m);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
if (x > y) swap(x, y);
if (!H[make_pair(x, y)]) {
H[make_pair(x, y)] = true;
b[x + 1] --, b[y] ++;
}
}
for (int i = 1; i <= n; i ++) b[i] += b[i - 1];
for (int i = 1; i <= n; i ++) b[i] += h;
for (int i = 1; i <= n; i ++) printf("%d\n", b[i]);
return 0;
}
0x04 二分
AcWing102. 最佳牛围栏
简化题意为在数组 $A$ 中找到一个长度不小于 $L$ 的连续子段,且该子段平均值最大。
二分答案,将问题转换为判断平均值 $x$ 是否合法,即是否存在长度不小于 $L$ 的连续子段的平均值 $\geq x$。
我们先把 $A$ 中的每一个数都减去 $x$,问题再次转换为是否存在长度不小于 $L$ 的连续子段的总和 $\geq 0$。
考虑前缀和,$S_i = A_1 + … + A_i$。朴素地可以枚举子段的两端点,运用前缀和进行计算。
但这种做法一定会超时,我们考虑优化。
我们先把答案表示出来。
$\underset{r - l \geq L}\max(A_{l + 1}, A_l + 1, …, A_r) = \underset{L\leq r\leq n}\max(S_r - \underset{0\leq l \leq r - L}\min(S_l))$
我们可以发现 $r$ 每增加 $1$,$l$ 也只会增加 $1$,所以我们不用每次都枚举 $l$,可以维护 $s_l$ 的最小值 $minl$,然后判断当前的 $s_r - minl$ 是否 $\geq 0$ 即可。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, L;
int a[N];
double s[N];
bool check(double x) {
for (int i = 1; i <= n; i ++) s[i] = a[i] - x;
for (int i = 1; i <= n; i ++) s[i] += s[i - 1];
double minn = 0x3f3f3f3f;
for (int i = 0, j = L; j <= n; i ++, j ++) {
minn = min(minn, s[i]);
if (s[j] - minn >= 0) return true;
}
return false;
}
int main() {
double l = 0, r = 0;
scanf("%d%d", &n, &L);
for (int i = 1; i <= n; i ++) {
scanf("%d", &a[i]);
r = max(r, (double)(a[i]));
}
while (r - l > 1e-6) {
double mid = (l + r) / 2;
if (check(mid)) l = mid;
else r = mid;
}
printf("%d\n", (int)(r * 1000));
return 0;
}
AcWing113. 特殊排序
假设当前已经排好了 $1,2,…,k$ 的顺序,考虑当前第 $k+1$ 个元素应该插入的位置。
我们可以二分插入位置 $mid$,如果 $mid$ 比 $i$ 小,那么 $l = mid$, 否则 $r = mid - 1$。
可以证明如此二分一定能成功插入,证明如下:
如果第 $k$ 个元素比第 $mid$ 个元素小,那么我们可以寻找第 $mid - 1$ 个元素。如果第 $k$ 个元素比第 $mid-1$ 个元素大,那么第 $k$ 个元素就插入到 $mid - 1$ 和 $mid - 2$ 之间;否则我们就继续往前找,直到第 $1$ 个元素,如果比第 $1$ 个元素小,那我们就插在第 $1$ 个元素前面。
反之,若第 $k$ 个元素大于第 $mid$ 个元素,同上亦可证明。
虽然我们二分时不会像上方一个一个枚举,但也足够证明二分的正确性。
// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.
class Solution {
public:
vector<int> specialSort(int N) {
vector<int> res(1, 1);
for (int i = 2; i <= N; i ++) {
int l = 0, r = res.size() - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (compare(res[mid], i)) l = mid;
else r = mid - 1;
}
res.push_back(i);
for (int j = res.size() - 2; j > r; j --) swap(res[j], res[j + 1]);
if (compare(i, res[r])) swap(res[r], res[r + 1]);
}
return res;
}
};
0x05 排序
AcWing103. 电影
使用 $map$ 存储每种语言能使多少个人开心,接着把每台电影语言和字幕让人开心的数量存入结构体 $v$ 中,接着以语言为主要,字幕为次要从大到小排序,v[1] 就是答案。
由于题目要求输出编号,所以还要加入 $id$ 存储电影序号。
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
const int N = 200010;
int n, m;
int a[N], b[N], c[N];
map<int, int> h;
struct node {
int x, y, id;
} v[N];
bool cmp(node a, node b) {
return a.x > b.x || a.x == b.x && a.y > b.y;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++) {
scanf("%d", &a[i]);
h[a[i]] ++;
}
scanf("%d", &m);
for (int i = 1; i <= m; i ++) scanf("%d", &b[i]);
for (int i = 1; i <= m; i ++) scanf("%d", &c[i]);
for (int i = 1; i <= m; i ++)
v[i] = {h[b[i]], h[c[i]], i};
sort(v + 1, v + 1 + m, cmp);
printf("%d\n", v[1].id);
return 0;
}
AcWing104. 货仓选址
超级经典的初中数学题。
现将 $A$ 从小到大进行排序,设货仓建在 $x$,$x$ 左侧有 $p$ 家店,右侧有 $q$ 家店。
- 如果 $p < q$,那么 $x$ 每右移一个单位长度,距离之和就会变小 $q - p$
- 如果 $p > q$,那么 $x$ 每左移一个单位长度,距离之和就会变小 $p - q$
所以,我们应该将店设在最中间,即中位数。具体地,如果 $n$ 是奇数,那货仓就建在 $A_{\frac{n + 1}{2}}$ 处;如果 $n$ 是偶数,那货仓就可以建在 $[A_\frac{n}{2}, A_\frac{n+1}{2}]$ 上的任意位置。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, a[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
sort(a + 1, a + 1 + n);
int m = (1 + n) / 2;
long long ans = 0;
for (int i = 1; i <= n; i ++) ans += abs(a[i] - a[m]);
printf("%d\n", ans);
return 0;
}
AcWing105. 七夕祭
首先我们可以发现,我们只会交换相邻的两个数,所以我们可以把行和列分开来做。
接着考虑对于数组 $a_1, a_2, …, a_n$ 的最小交换次数。
先思考当前 $1$ 和 $n$ 不能互相交换的情况。
由于最后 $a$ 中的每个数都要变为 $a$ 的平均值 $\overline{x}$,所以我们记 $c_i = a_i - \overline{x}$,然后我们用一个前缀和数组 $S$,记录 $c$ 的前缀和。
那么 $\sum_{i = 1}^{n} |S_i|$ 即为答案。
为什么是这样的呢?我们可以举一个例子。
$A: 1\ 3\ 2\ 7\ 7$
$C: -3 -1 -2\ 3\ 3$
$S: -3 -4 -6 -3\ 0$
发现了吗?$S_1$ 记录了 $C_1$ 应该被 $C_2$ 给 $3$,但是 $C_2$ 本身就是 $-1$,又要考虑给 $C_1$ 的问题,所以 $C_2$ 总共需要 $C_3$ 给它 $4$,$C_3$ 同理,需要 $C_4$ 的 $6$。到了 $C_4$,它本身拥有 $3$,所以还需要 $C_5$ 给它 $3$。
这样子我们就可以不重不漏地计算出答案。
回到本题,从上述做法的线性改为了环形。注意到(注意力惊人)一定存在最优解不是环而是链,所以我们可以枚举环的断点,用链的做法去做。
证明如下:
来自 @AcWing 东边的西瓜皮
我们假设断点为 $k$,那么原前缀和序列的顺序就成了 $S_{k+1},…,S_n,S_1,…,S_k$,我们考虑修改过后的前缀和数组,即为 $G$。
$G_{k + 1} = S_{k + 1} - S_k$
$G_{k + 2} = S_{k + 2} - S_k$
$…$
$G_n = S_n - S_k$
$G_1 = S_1 + S_n - S_k$
$G_2 = S_2 + S_n - S_k$
$…$
$G_k = S_k + S_n - S_k$
由于 $S_n$ 为 $0$,所以 $G_i = S_i - S_k$
所以我们要找出使得 $\sum_{i = 1}^{n}|S_i - S_k|$ 最小的 $k$ 即可。这很明显是货仓选址问题,所以 $k = \frac{(n + 1)}{2}$
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m, T;
int row[N], col[N];
int a[N], b[N];
int main() {
scanf("%d%d%d", &n, &m, &T);
while (T --) {
int x, y;
scanf("%d%d", &x, &y);
row[x] ++, col[y] ++;
}
int averow = 0, avecol = 0;
for (int i = 1; i <= n; i ++) averow += row[i];
for (int i = 1; i <= m; i ++) avecol += col[i];
bool f1 = true, f2 = true;
if (averow % n != 0) f1 = false;
if (avecol % m != 0) f2 = false;
if (!f1 && !f2) {
printf("impossible");
return 0;
} else if (!f1) {
printf("column ");
} else if (!f2) {
printf("row ");
} else {
printf("both ");
}
long long ans = 0;
if (f1) {
averow /= n;
a[1] = 0;
for (int i = 2; i <= n; i ++) a[i] = a[i - 1] + row[i] - averow;
sort(a + 1, a + 1 + n);
long long res = 0;
for (int i = 1; i <= n; i ++)
res += abs(a[i] - a[n + 1 >> 1]);
ans += res;
}
if (f2) {
avecol /= m;
b[1] = 0;
for (int i = 2; i <= m; i ++) b[i] = b[i - 1] + col[i] - avecol;
sort(b + 1, b + 1 + m);
long long res = 0;
for (int i = 1; i <= m; i ++)
res += abs(b[i] - b[m + 1 >> 1]);
ans += res;
}
printf("%lld\n", ans);
return 0;
}
AcWing106. 动态中位数
对顶堆算法。
用一个大根堆和一个小根堆来维护数据,做法是如果新加入的数据大于大根堆的堆顶,就把它加入小根堆,否则加入大根堆。
加入完后,我们还要对大根堆和小根堆进行维护,使得大根堆长度为小根堆长度加一。
我们只要在 $n$ 为奇数时访问大根堆的堆顶即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int T, p, n;
int a[N];
int main() {
scanf("%d", &T);
while (T --) {
scanf("%d%d", &p, &n);
printf("%d %d\n", p, (n + 1) / 2);
int cnt = 0;
priority_queue<int> down;
priority_queue<int, vector<int>, greater<int>> up;
for (int i = 1; i <= n; i ++) {
int x; scanf("%d", &x);
if (down.empty() or x <= down.top()) down.push(x);
else up.push(x);
if (down.size() > up.size() + 1) up.push(down.top()), down.pop();
if (up.size() > down.size()) down.push(up.top()), up.pop();
if (i & 1) {
printf("%d ", down.top());
cnt ++;
if (cnt % 10 == 0) puts("");
}
}
if (cnt % 10) puts("");
}
return 0;
}
AcWing108. 奇数码问题
考虑将二维数组写成类似 $[1, 2, 3, 4, 5, 6, 7, 8]$ 的形式,则此时左右交换不会影响此序列。上下交换,比如交换 $4$ 和 $7$,则会增加两个逆序对。我们可以拓展到 $n\times n$ 的矩阵中,即上下交换会增加 $n - 1$ 个逆序对。
因为 $n$ 是奇数,所以 $n - 1$ 一定是偶数,所以如果初始序列有奇数个逆序对,则不论我们怎么操作,最终都只有奇数个逆序对,反之亦然。
所以我们可以分别计算输入序列和答案序列的逆序对,判断它们的奇偶性是否相同。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long LL;
const int N = 500010;
int n, q[N], tmp[N];
LL merge_sort(int l, int r)
{
if (l >= r) return 0;
int mid = l + r >> 1;
LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++] = q[i ++];
else
{
tmp[k ++] = q[j ++];
res += mid - i + 1;
}
while (i <= mid)
tmp[k ++] = q[i ++];
while (j <= r)
tmp[k ++] = q[j ++];
for (int i = l, j = 0; i <= r; i ++, j ++)
q[i] = tmp[j];
return res;
}
int main()
{
while (cin >> n) {
int len = 0;
for (int i = 1; i <= n * n; i ++) {
int x; cin >> x;
if (x) q[len ++] = x;
}
LL res1 = merge_sort(0, n * n - 2);
len = 0;
for (int i = 1; i <= n * n; i ++) {
int x; cin >> x;
if (x) q[len ++] = x;
}
LL res2 = merge_sort(0, n * n - 2);
if ((res1 & 1) == (res2 & 1)) puts("TAK");
else puts("NIE");
}
return 0;
}
0x06 倍增
AcWing 109.天才ACM
倍增。
最开始 $l = 0$,然后进行如下操作:
1. 定义变量 $r = l, p = 1$
2. 循环判断 $[l, r + p)$ 的校验值是否小于等于 $T$。
- 如果是,r += p, p *= 2
- 如果不是,p /= 2
3. 当 $p = 0$ 时,退出循环,让 $l = r$
接着我们考虑如何判断校验值是否小于等于 $T$。
一个显而易见的结论是,如果序列 $A$ 是从小到大排序的,那么校验值就应该是 $(A_n - A_1) ^ 2 + (A_{n - 1} - A_2) ^ 2 + …$
即先让最大值和最小值凑一对,然后是次大和次小,并且我们配的对数量要小于 $m$。
所以,假设当前要计算 $[l, r)$ 的最大值,我们只要将 $[l,r)$ 从小到大排序,做如上操作即可。
分析下时间复杂度,设每个答案的长度为 $len_1,len_2,…,len_k$,那么对于每个 $len_i$,需要倍增 $O(logn)$。
那么总共的答案就是 $O(logn \times len_1 log len_1 + logn \times len_2 log len_2 + … + logn \times len_k log len_k)= O(logn(len_1loglen_1) + … + len_kloglen_k)=O(n^2logn)$
这个复杂度是一定会超时的,所以我们需要优化。
注意到在处理 $[l,r)$ 时,已经把 $[l, r)$ 排好了序,所以我们在处理 $[l, r + p)$ 时就不用
重新排序,只要将 $[r, r + p)$ 排序,然后和 $[l, r)$ 进行归并即可。
这种思路下只需要将每个区间处理一次,时间复杂度就是 $O(len_1loglen_1 + … + len_kloglen_k) \leq O(nlogn)$,可以通过本题。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 500010;
int T, n, m;
LL t;
int w[N], b[N], tmp[N];
bool check(int l, int mid, int r) {
int k = 0;
for (int i = mid; i < r; i ++) b[i] = w[i];
sort(b + mid, b + r);
int i = l, j = mid;
while (i < mid && j < r)
if (b[i] < b[j]) tmp[k ++] = b[i ++];
else tmp[k ++] = b[j ++];
while (i < mid) tmp[k ++] = b[i ++];
while (j < r) tmp[k ++] = b[j ++];
LL res = 0;
for (int i = 0; i < m && i < k; i ++, k --)
res += (LL)(tmp[k - 1] - tmp[i]) * (tmp[k - 1] - tmp[i]);
return res <= t;
}
int main() {
scanf("%d", &T);
while (T --) {
scanf("%d%d%lld", &n, &m, &t);
for (int i = 0; i < n; i ++) scanf("%d", &w[i]);
int l = 0, cnt = 0;
while (l < n) {
int r = l, p = 1;
while (p) {
if (r + p <= n && check(l, r, r + p)) {
r += p;
p <<= 1;
for (int i = l; i < r; i ++)
b[i] = tmp[i - l];
} else {
p >>= 1;
}
}
cnt ++;
l = r;
}
printf("%d\n", cnt);
}
return 0;
}
0x07 贪心
AcWing1055. 股票买卖
考虑当前是第 $i$ 天,分两种情况。
1. 当前持有股票,则若下一天是涨,我们肯定会把股票留着,否则,我们应该直接卖出。
2. 当前未持有股票,如果下一天涨,我们应该在今天买入,否则不应该买入。
所以可以得到 $ans = \sum_{i = 2}^{n}\max(primes_i - primes_{i - 1}, 0)$
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, w[N];
int f[N][2];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);
int res = 0;
for (int i = 2; i <= n; i ++)
res += max(w[i] - w[i - 1], 0);
printf("%d\n", res);
return 0;
}
AcWing110. 防晒
首先把每一头牛可接受的光线按 $minSPF$ 为第一关键字,$maxSPF$ 为第二关键字,从大到小排序。
接着分别枚举每头牛可用的防晒霜,对于每头牛选择 $SPF$ 最大的防晒霜。
证明:
首先,对于每一罐防晒霜 $SPF_i$,因为我们已经按照 $minSPF$ 进行了排序,所以如果
防晒霜 $SPF_x$,大于 $minSPF_{i}$,则它一定大于 $minSPF_{i + 1}$ ~ $minSPF_{n}$。
那么对于一头奶牛 $i$ 与防晒霜 $x$ 和 $y$ $(x < y)$ 来说,只有以下三种情况:
- $x$ 能用,$y$ 能用
- $x$ 能用,$y$ 不能用
- $x$ 不能用,$y$ 不能用
所以 $x$ 的适用范围比 $y$ 更广,故而我们应该尽可能先使用 $y$,实在不行再考虑 $x$。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 2510;
int c, l;
PII w[N];
int spf[N], cov[N];
int main() {
scanf("%d%d", &c, &l);
for (int i = 1; i <= c; i ++)
scanf("%d%d", &w[i].first, &w[i].second);
for (int i = 1; i <= l; i ++)
scanf("%d%d", &spf[i], &cov[i]);
sort(w + 1, w + 1 + c, [&](PII a, PII b) {
return a.first > b.first;
});
int ans = 0;
for (int i = 1; i <= c; i ++) {
int sel = 0;
for (int j = 1; j <= l; j ++) {
if (w[i].first <= spf[j] && spf[j] <= w[i].second && cov[j] && spf[j] > spf[sel])
sel = j;
}
if (sel) ans ++, cov[sel] --;
}
printf("%d\n", ans);
return 0;
}
AcWing111. 畜栏预定
首先对于每头牛,按照吃草的开始时间排序,然后从前到后考虑每只牛,用一个小根堆来枚举当前结束时间最早的畜栏。
对于一头牛,如果它吃草的开始时间比小根堆里所有的结束时间都早(即早于堆顶),就要新开辟一个畜栏。
否则,我们应该将其放入当前任意可放入的畜栏,方便起见,放入堆顶。
证明(来自 $yxc$,非常精妙):
反证法,假设存在一种方案,使得需要的畜栏数量更少,记其需要的畜栏数量是 $m$。
考虑在上述做法中,第一次新建第 $m+1$ 个畜栏的时刻,不妨设当前处理的是第 $i$头牛。
由于所有牛是按开始时间从小到大排好序的,所以现在前 $m$ 个畜栏中最后一头牛的开始时间一定小于等于第 $i$
头牛的开始时间。
而且前 $m$ 个畜栏中最小的结束时间大于等于第 $i$ 头牛的开始时间,所以前 $m$
个畜栏里最后一头牛的吃草区间一定都包含第 $i$ 头牛的开始时间,所以我们就找到了 $m+1$
个区间存在交集,所以至少需要 $m+1$ 个畜栏,矛盾。
所以上述做法可以得到最优解,证毕。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 50010;
int n, cnt;
int ans[N];
priority_queue<PII, vector<PII>, greater<PII>> q;
struct node {
int l, r, id;
} w[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
scanf("%d%d", &w[i].l, &w[i].r);
for (int i = 1; i <= n; i ++)
w[i].id = i;
sort(w + 1, w + 1 + n, [&](node a, node b) {
return a.l < b.l;
});
int res = 0;
for (int i = 1; i <= n; i ++) {
if (q.empty() || w[i].l <= q.top().first) {
q.push({w[i].r, ++ res});
ans[w[i].id] = res;
} else {
PII t = q.top(); q.pop();
q.push({w[i].r, t.second});
ans[w[i].id] = t.second;
}
}
printf("%d\n", res);
for (int i = 1; i <= n; i ++)
printf("%d\n", ans[i]);
return 0;
}
AcWing112. 雷达设备
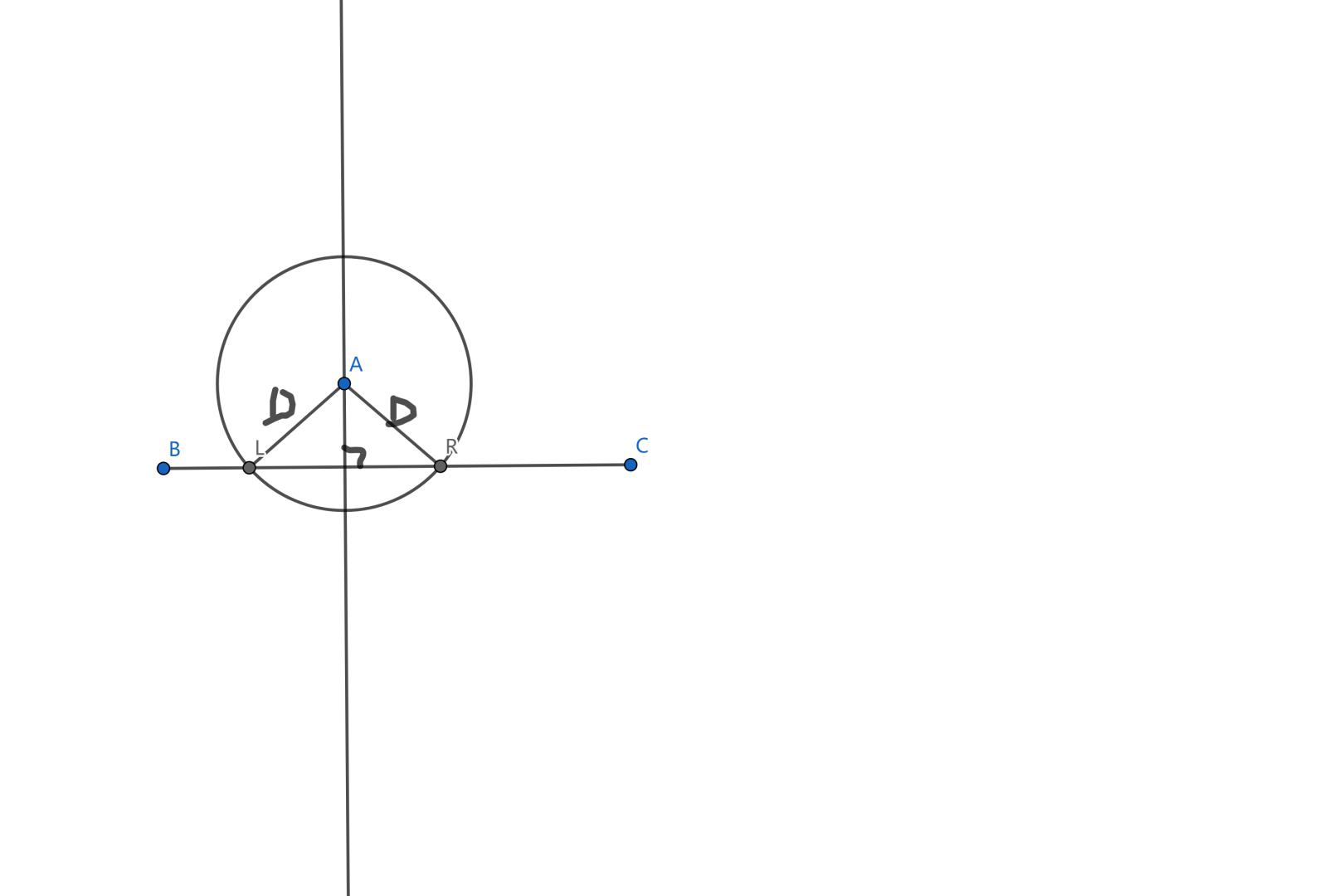
如图,我们求出对于每个点 $(x, y)$,能覆盖它的范围 $[l,r]$,根据勾股定理我们可以得到:
$l = y - \sqrt{D ^ 2 - x^2}, r = y + \sqrt{D^2 - x^2}$
于是问题就转化成了,给定 $n$ 个区间,在 $x$ 上找尽量少的点,使每个区间内至少有一个点。
这就是 AcWing905. 区间选点,模板题。
我们把每个区间按 $r$ 排序,对于每个区间:
- 如果区间内已经有了点,就跳过这个区间。
- 如果区间内没有点,就在区间的右端点找点。
正确性显然,不予证明。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef pair<double, double> PDD;
const int N = 1010;
int n, d;
PDD q[N];
PDD calc(int x, int y) {
if (d * d < y * y) return {0x3f3f3f3f, 0x3f3f3f3f};
double l = x - sqrt(d * d - y * y);
double r = x + sqrt(d * d - y * y);
return {l, r};
}
int main() {
scanf("%d%d", &n, &d);
for (int i = 1; i <= n; i ++) {
int x, y;
scanf("%d%d", &x, &y);
q[i] = calc(x, y);
if (q[i].first == 0x3f3f3f3f) {
puts("-1");
return 0;
}
}
sort(q + 1, q + 1 + n, [&](PDD a, PDD b) {
return a.second < b.second;
});
int cnt = 0;
double ed = -0x3f3f3f3f;
for (int i = 1; i <= n; i ++) {
if (ed < q[i].first) {
cnt ++;
ed = q[i].second;
}
}
printf("%d\n", cnt);
return 0;
}
AcWing114. 国王游戏
作法:把所有人按照 $a \times b$ 从小到大排序,然后循环找最大值。
证明:
假设当前有两个人 $i$ 和 $i + 1$,考虑如果排序前和排序后的答案。
这里假设国王为 $0$ 号大臣。
-
排序前,即 $a_i \times b_i > a_{i+1} \times b_{i+1}$
此时大臣 $i$ 的奖赏是:$\frac{\prod_{j = 0}^{i - 1}a_j}{b_i}$
此时大臣 $i + 1$ 的奖赏是:$\frac{\prod_{j = 0}^{i}a_j}{b_{i + 1}}$
-
排序后,即 $a_{i+1} \times b_{i+1} > a_i \times b_i$
此时大臣 $i$ 的奖赏是:$\frac{(\prod_{j = 0}^{i-1}a_j) \times a_{i + 1}}{b_i}$
此时大臣 $i + 1$ 的奖赏是:$\frac{\prod_{j = 0}^{i-1}a_j}{b_{i + 1}}$
把每个式子都提取公因式 $\prod_{j = 0}^{i - 1}a_j$,再乘上 $b_i \times b_{i + 1}$,
转为求:$\max(b_{i + 1}, a_i \times b_i)$ 与 $\max(b_i, a_{i + 1} \times b_{i + 1})$ 的最大值
通过推导可以得出,当 $a_i \times b_i < a_{i + 1} \times b_{i + 1}$ 时,交换前更优;
反之,交换后更优。所以无论如何我们都应该按照 $a_i \times b_i$ 排序。
要写高精度!!!!!!!!!!!!!(烦死)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 1010, M = 4010;
int n;
PII w[N];
void mul(int a[], int b) {
for (int i = 0, t = 0; i < M; i ++) {
t += a[i] * b;
a[i] = t % 10;
t /= 10;
}
}
void div(int c[], int a[], int b) {
for (int i = M - 1, r = 0; i >= 0; i --) {
r = r * 10 + a[i];
c[i] = r / b;
r %= b;
}
}
int compare(int a[], int b[]) {
for (int i = M - 1; i >= 0; i --)
if (a[i] > b[i]) return 1;
else if (a[i] < b[i]) return -1;
return 0;
}
void print(int a[]) {
int l = M - 1;
while (a[l] == 0 && l > 0) l --;
for (int i = l; i >= 0; i --)
printf("%d", a[i]);
}
int main() {
scanf("%d", &n);
for (int i = 0; i <= n; i ++)
scanf("%d%d", &w[i].x, &w[i].y);
sort(w + 1, w + 1 + n, [&](PII a, PII b) {
return a.x * a.y < b.x * b.y;
});
int tmp[M], p[M] = {1}, res[M] = {0};
for (int i = 1; i <= n; i ++) {
mul(p, w[i - 1].x);
div(tmp, p, w[i].y);
if (compare(res, tmp) == -1)
memcpy(res, tmp, sizeof tmp);
}
print(res);
return 0;
}
AcWing115. 给树染色
首先我们考虑没有限制的情况,那我们从大到小来取,现在有了限制,我们照样可以利用类似的思路。
假设当前最大值为 $a$,它的父节点为 $b$,那么 $a$ 和 $b$ 取的顺序一定是相邻的,所以我们可以把它们当作一个点来做。
那么如果现在又有一个点 $c$,那我们有两种染法:
- 先 $a,b$,再 $c$:$S_1 = a + 2b + 3c$
- 先 $c$,再 $a, b$:$S_2 = c + 2a + 3b$
我们考虑作差:$S_1 - S_2 = a + 2b + 3c - c - 2a - 3b = 2c - (a + b) = 2(c - \frac{a + b}{2})$
所以当 $c>\frac{a+b}{2}$ 时 我们应该先染式子右边,否则先染式子左边。
我们考虑是否能把其拓展为两个序列。
假设有两个序列 $a_1,a_2,…a_n$ 和 $b_1,b_2,…,b_m$。
与之相似我们也有两种染法:
- $S_1 = \sum_{i = 1}^{n}a_i \times i + \sum_{i = n + 1}^{n + m}b_i \times i$
- $S_2 = \sum_{i = 1}^{m}b_i \times i + \sum_{i = m + 1}^{n + m}a_i \times i$
作差:$S_1 - S_2 = n \sum_{i = 1}^{m}b_i - m \sum_{i = 1}^{n}a_i$
所以当 $S_1 < S_2$ 时,$\frac{\sum_{i = 1}^{m}b_i}{m} < \frac{\sum_{i = 1}^{n}a_i}{n}$
,反之亦然。
因此,我们可以把 $a$ 序列和 $b$ 序列看作点权为 $a$ 的平均值和 $b$ 的平均值的两个点。
我们最后的做法是:每次寻找当前树上的最大值,然后找到它的父亲,在合并顺序中把最大值跟在父亲的后面,最后用最大值的点权更新父亲。
考虑如何计算这种合并方式的代价。
首先最开始先加上每个点的点权。对于当前要合并的 $a$ 和 $b$,如果把 $b$ 放在 $a$ 的后面,就代表一整个 $b$ 都要加上一个偏移量 $k$。
由以上推导可以发现,偏移量其实就是 $a$ 中点的数量,所以代价就应该加上 $a$ 中点的数量乘以 $b$ 中点权的总和。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, root;
struct Node {
int p, s, size;
double avg;
} nodes[N];
int find() {
int res = 0;
for (int i = 1; i <= n; i ++)
if (i != root && nodes[i].avg > nodes[res].avg)
res = i;
return res;
}
int main() {
int ans = 0;
scanf("%d%d", &n, &root);
for (int i = 1; i <= n; i ++) {
scanf("%d", &nodes[i].s);
nodes[i].avg = nodes[i].s;
nodes[i].size = 1;
ans += nodes[i].s;
}
for (int i = 1; i < n; i ++) {
int u, v;
scanf("%d%d", &u, &v);
nodes[v].p = u;
}
for (int i = 1; i < n; i ++) {
int p = find();
int fa = nodes[p].p;
ans += nodes[fa].size * nodes[p].s;
for (int j = 1; j <= n; j ++)
if (nodes[j].p == p)
nodes[j].p = fa;
nodes[fa].size += nodes[p].size;
nodes[fa].s += nodes[p].s;
nodes[fa].avg = (double)nodes[fa].s / nodes[fa].size;
nodes[p].avg = -1;
}
printf("%d\n", ans);
return 0;
}


更完了,好耶ヾ(✿゚▽゚)ノ
AcWing为什么不支持
<font color=""></font>?加油。
啊!?怎么是天元弟。
诶嘿