【-1】前言

仅为本人后期复习提供需要，如有笔误请忽略。

【1】KMP 算法实现原理

KMP 算法是干什么的？

先扔 一道题，KMP 算法是比较一个字符串在另一个字符串中出现位置的。

我们先考虑朴素解法，不妨设文本串为 $a$，模式串为 $b$，我们枚举 $a$ 的每一位，再枚举 $b$ 的每一位，如果发现两串一点不匹配，$a$ 向前一位，$b$ 重新开始枚举，这是很萌萌的新手做法，时间复杂度 $O(nm)$，在范围 $1\le|a|,|b|\le10^5$ 往上的题目中不可取。

KMP 配对求法

我们考虑优化，先扔一个样例。

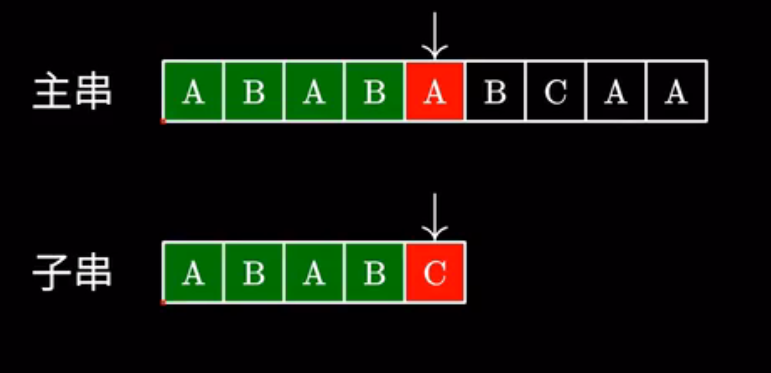
我们还是按照刚才的方法匹配，发现最后一个字符不匹配，但是我们发现前面这些字符已经匹配好了，我们能不能合理利用他们来优化时间复杂度呢？

这就有了我们 $\text{KMP}$ 算法。$\text{KMP}$ 算法意在用一个数组 $\text{next}$ 来避免重复比较。

$\text{next}$ 数组就是一旦一个字母失配之后，让$i$ 前进 $next_{j - 1}$ 个位置，这个位置就是避免重复比较的位置，我们等一下说 $\text{next}$ 怎么求，我们先说 $\text{KMP}$ 的匹配过程，并帮大家理解 $\text{next}$ 数组有什么用。

这样说比较难理解，我们扔个图。

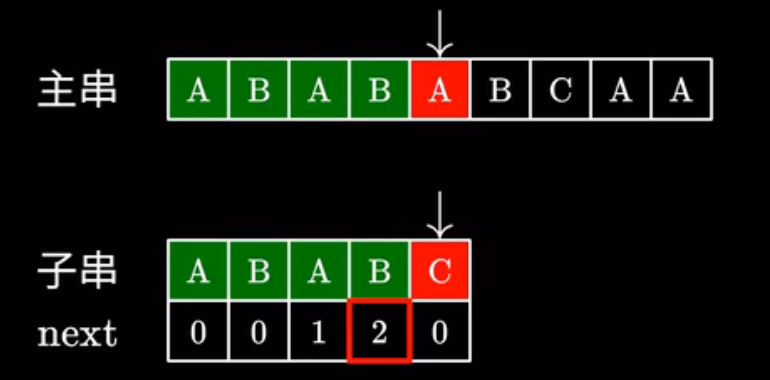
比如说我们第 $j$ 个位置失配了，我们让 $i$ 指针前进 $2$ 个单位长度（即 $next_{j - 1}$），这样就避免了重复配对情况。就像下图。

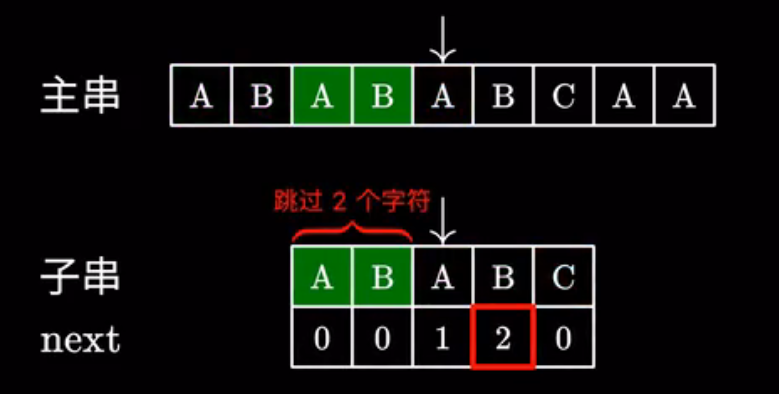
然后指针继续往后扫，这样时间复杂度就变成线性的了。

给出配对代码：

void KMP()
{
    int p = 0;
    for(int i = 1;i <= lena;i ++ ){
        while(p && b[p + 1] != a[i]) p = nxt[p];
        if(a[i] == b[p + 1]) p ++ ;
        if(p == lenb){
            cout << i - p + 1 << endl;
            p = nxt[p];
        }
    }
}

$\text{next}$ 数组怎么求?

我们还是看上面这张图，我们发现跳过的这两个 $\text{AB}$ 和失配前最后两个 $\text{AB}$ 是一样的，换句话来说，对 $b$ 串前 $4$ 个字符，他们拥有一个共同的前缀和后缀 $\text{AB}$，所以我们发现，$\text{next}$ 数组的本质，就是寻找子串中“最长相同前后缀的长度”。

那我们如何找到子串中“最长相同前后缀的长度”呢？还需要暴力吗？当然不需要，我们只要每当进入一个字符，判断前面一个字符串的最长相同前缀的后面一个是不是进入的字符就行了，比如说我们已经处理好这两个字符的最长相同前后缀了：

下面加入一个字符 $\text{A}$，会发现正好又构成了一个最长相同前后缀 $\text{ABA}$。

那么如果加入的字符没这么巧呢？

比如运行到这一步，我们发现无法凑巧简单地构成前后缀，那怎么办呢？我们考虑更短的前后缀，通过前面的操作，我们可以知道，绿色的这两个部分应该是完全相同，即他们的后缀也完全相同。我们再来看第一个绿色部分，我们也可以知道他也是有最长相同前后缀的，就是 $\text{A}$，这个直接查表就可以知道，通过刚才那个结论，我们就知道这两个 $\text{A}$ 相等，就是：

然后又回到那个快乐的操作了，我们现在看加上下一个字符是否构成最长相等前后缀即可，这里就是 $\text{AB}$。

这就是 $\text{KMP}$ 算法全部内容，时间复杂度 $O(n+m)$，很优秀。

给出预处理 $\text{next}$ 数组部分代码：

void get_nxt()
{
    int p = 0;
    nxt[1] = 0;
    for(int i = 2;i <= lenb;i ++ ){
        while(p && b[p + 1] != b[i]) p = nxt[p];
        if(b[i] == b[p + 1]) p ++ ;
        nxt[i] = p;
    }
}

【2】模板代码

这题还是有细节要注意的，下标从 $1$ 开始。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 5;
int nxt[N], lena, lenb;
char a[N], b[N];
void get_nxt()
{
    int p = 0;
    nxt[1] = 0;
    for(int i = 2;i <= lenb;i ++ ){
        while(p && b[p + 1] != b[i]) p = nxt[p];
        if(b[i] == b[p + 1]) p ++ ;
        nxt[i] = p;
    }
}
void KMP()
{
    int p = 0;
    for(int i = 1;i <= lena;i ++ ){
        while(p && b[p + 1] != a[i]) p = nxt[p];
        if(a[i] == b[p + 1]) p ++ ;
        if(p == lenb){
            cout << i - p + 1 << endl;
            p = nxt[p];
        }
    }
}
int main()
{
    cin >> a + 1 >> b + 1;
    lena = strlen(a + 1), lenb = strlen(b + 1);
    get_nxt();
    KMP();
    for(int i = 1;i <= lenb;i ++ ) cout << nxt[i] << ' ';
    return 0;
}

【-2】结语

参考资料
- 最浅显易懂的 KMP 算法讲解 - 奇乐编程学院bilibili。