背包九讲笔记

作者： 作者的头像   天元之弈 ,  2024-10-02 20:51:40 ,  所有人可见 ,  阅读 15

5


1

PS: 几万年前的笔记qwq

背包问题

1. 01背包

状态表示： $f_{i,j}$

  • 集合：考虑前 $i$ 个物品，总体积不超过 $j$ 的方案集合
  • 属性：最大值 $\max$
  • 答案：$f_{n,m}$

状态计算：

  • 选第 $i$ 个物品，那么我们曲线救国可得 $f_{i,j} = f_{i-1, j - v_i} + w_i$
  • 不选第 $i$ 个物品，即 $f_{i,j} = f_{i - 1,j}$

所以我们总的状态转移方程为两者的最大值，即：

$$f_{i,j} = \max(f_{i - 1,j}, f_{i-1, j - v_i} + w_i)$$

因为我们不是每一次 $j - v_i$ 都 $>0$，所以将两个式子分开处理。

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i ++)   
        for (int j = 1; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

时间复杂度：$O(nm)$，空间复杂度：$O(nm)$

注意到每一次 $DP$ 实际上只用到了上一维的结果，所以我们可以优化掉一层数组，即：

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) {
        int v, w;
        cin >> v >> w;
        for (int j = m; j >= v; j --)
            f[j] = max(f[j], f[j - v] + w);
    }
    cout << f[m] << endl;
    return 0;
}

这里我们去掉了 $f$ 数组的第一维的同时，内层循环可以直接从 $v$ 遍历到 $m$，更为方便的同时，内循环顺序也变成了从大到小。

从大到小的原因是我们 $DP$ 所要用到的是 $i - 1$ 一层的 $f$，如果从小到大循环，那么在处理 $f_5$ 的时候，$f_{1,2,3,4}$ 可能已经发生了修改，我们就访问不到 $i - 1$ 层的 $f$ 了。所以这里我们选择从大到小地枚举。

2. 完全背包

状态表示：$f_{i,j}$

  • 集合：考虑前 $i$ 个物品，且总体积不超过 $j$ 的方案
  • 属性：$\max$

状态计算：

  • 考虑选 $k$ 个当前物品的情况，则根据 $01$ 背包的经验，应为 $f_{i - 1, j - k \times v_i} + w_i$

从而我们得出完全背包的朴素做法的状态转移方程：

$$f_{i,j} = \max(f_{i - 1,j}, f_{i - 1, j - k\times v_i} + w_i)$$

在具体计算的过程中，为了防止买超过背包容量的物品，所以要保证 $k \times v_i \leq j$。

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], f[N][N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++)
            for (int k = 0; k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
    printf("%d\n", f[n][m]);
    return 0;
}

时间复杂度：$O(nm^2)$

但三重循环的时间复杂度过于大了，无法通过评测，所以我们考虑优化。

注意到 $f_{i,j} = \max(f_{i - 1, j}, f_{i - 1,j - v} + w, f_{i - 1, j - 2v} + 2w, …, f_{i - 1, j - kv} + kw)$ （此处 $k$ 为满足 $kv \leq j$ 的最大值）

而 $f_{i,j-v} = \max(f_{i - 1, j - v}, f_{i - 1, j - 2v} + w, f_{i - 1, j - 3v} + 2w, …, f_{i - 1,j - kv} + (k-1)w)$

所以 $f_{i,j} = \max(f_{i - 1,j}, f_{i, j - v} + w)$

这里会有一个问题：为什么两个式子的最后一项都是 $kv$呢？

我们可以观察 $kv \leq j$ 这个式子，将 $j - v$ 代入 $j$ 实际上就是：$$kv \leq j - v$$，移项便可得到 $(k+1)v \leq j$。

所以在这个式子中的 $k_{max}$ 会比 $kv \leq j$ 中的 $k_{max}$ 少 $1$，而 $f_{i, j - v}$ 天生就多减了一个 $v$。

所以 $f_{i - 1,j - kv} + (k - 1)w$ 其实是由 $f_{i - 1, j - (k - 1)v - v} + (k - 1)w$ 得来的。

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], f[N][N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

根据 $01$ 背包的经验，我们同样可以将完全背包也优化成一维。

#include <cstdio>
#include <algorithm>
const int N = 1010;
int n, m;
int f[N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) {
        int v, w;
        scanf("%d%d", &v, &w);
        for (int j = v; j <= m; j ++)
            f[j] = std::max(f[j], f[j - v] + w);
    }
    printf("%d\n", f[m]);
    return 0;
}

这里的循环就是从小到大了，因为我们用到的就是 $i$ 这层的数据，而在 $01$ 背包中，我们用到的是 $i - 1$ 的数据。

时间复杂度：$O(nm)$

3. 多重背包

朴素做法

类似于完全背包的朴素做法，再加一个物品数量的判定即可。

#include <iostream>
using namespace std;
const int N = 105;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
            for (int k = 0; k * v[i] <= j && k <= s[i]; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
    cout << f[n][m] << endl;
    return 0;
}

时间复杂度：$O(nms)$

二进制优化

同样类似于完全背包，多重背包的朴素做法同样是三层循环，也同样会超时。

我们考虑通过二进制枚举优化第三层循环。

这里的二进制优化指的是将物品数量拆分成形如 $2^{0} + 2^{1} + … + 2^{k} + t$ 这种形式，举个例子，$27 = 1 + 2 + 4 + 8 + 12$

我们发现，$1$ ~ $27$ 的所有数字都可以通过 $1、2、4、8、12$ 凑出来，如此我们便可以把数量为 $27$ 的物品拆分成体积和价值则分别为 $v, 2v, 4v…$ 和 $w,2w,4w,…$ 的物品，这样就忽略了数量这一因素，拆分完成后，我们便可以用 $01$ 背包的思路进行 $DP$。

#include <iostream>
using namespace std;
const int N = 12010, M = 2010;
int n, m, cnt;
int v[N], w[N];
int f[M];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) {
        int a, b, s;
        scanf("%d%d%d", &a, &b, &s);
        int k = 1;
        while (k <= s) {
            v[++ cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s) {
            v[++ cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    printf("%d\n", f[m]);
    return 0;
}

这是多重背包二进制优化的一种写法，后面混合背包中也会有更简单的写法。

时间复杂度：$O(nlogs·m)$

* 单调队列优化

令 $f_{i - 1, j} = f_j$，则：

  • $f_{i, r} = f_r$
  • $f_{i, r + v} = \max(f_{r + v}, f_{r} + w)$
  • $f_{i, r + 2v} = \max(f_{r + 2v}, f_{r + v} + w, f_r + 2w)$
  • $…$
  • $f_{i, r + (s - 1)v} = \max(f_{r + (s-1)v}, f_{r + (s - 2)v} + w, …, f_r + (s - 1)w)$
  • $f_{i, r + sv} = \max(f_{r + sv}, f_{r + (s - 1)v} + w, …, f_r + sw)$
  • $f_{i, r + (s + 1)v} = \max(f_{r + (s+1)v}, f_{r + sv} + w,…, f_{r + v} + sw)$
  • …
  • $f_{i, j - 2v} = \max(f_{j - 2v}, f_{j - 3v} + w, …, f_{j - (s+2)v} + sw)$
  • $f_{i, j-v} = \max(f_{j-v}, f_{j - 2v} + w, …, f_{j - (s + 1)v} + sw)$
  • $f_{i, j} = \max(f_j, f_{j - v} + w,…, f_{j - sv} + sw)$

其中 $r = j\;mod\;v$。

我们把 $\max$ 中的 $w$ 都先不看，可以很明显的发现 $\max$ 中 $f$ 的下标在 $f_{i,r+sv}$ 之后就在不断地做着滑动窗口，所以我们可以维护一个单调队列的，来计算最大值。

具体的，我们将 $j$ 根据除以 $v$ 的余数分组，每一组分别进行单调队列，就像上方的式子。

不要忘记，滑动窗口内部比较最大值的时候要加上偏移量 $w$，具体来说就是当前下标与最大值下标之间差了 $t$ 个 $v$，就要加上 $t$ 个 $w$。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010, M = 20010;
int n, m;
int v[N], w[N], s[N];
int f[N][M];
int q[M];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
    for (int i = 1; i <= n; i ++)
        for (int r = 0; r < v[i]; r ++) { // 枚举余数
            int hh = 0, tt = -1;
            for (int j = r; j <= m; j += v[i]) {
                while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++;// 太老的滚蛋
                // 比你老还没你强的滚蛋
                while (hh <= tt && f[i - 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <= f[i - 1][j]) tt --;
                q[++ tt] = j;
                f[i][j] = max(f[i][j], f[i - 1][q[hh]] + (j - q[hh]) / v[i] * w[i]);
            }
        }
    printf("%d\n", f[n][m]);
    return 0;
}

同样的，我们可以用滚动数组优化：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010, M = 20010;
int n, m;
int v[N], w[N], s[N];
int f[2][M];
int q[M];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
    for (int i = 1; i <= n; i ++)
        for (int r = 0; r < v[i]; r ++) {
            int hh = 0, tt = -1;
            for (int j = r; j <= m; j += v[i]) {
                while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++;
                while (hh <= tt && f[i - 1 & 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <= f[i - 1 & 1][j]) tt --;
                q[++ tt] = j;
                f[i & 1][j] = max(f[i & 1][j], f[i - 1 & 1][q[hh]] + (j - q[hh]) / v[i] * w[i]);
            }
        }
    printf("%d\n", f[n & 1][m]);
    return 0;
}

4. 分组背包

类似于 $01$ 背包问题，枚举一遍组内的物品选择哪个即可。

#include <iostream>
using namespace std;
const int N = 110;
int n, m;
int s[N], v[N][N], w[N][N];
int f[N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) {
        cin >> s[i];
        for (int j = 1; j <= s[i]; j ++)
            cin >> v[i][j] >> w[i][j];
    }
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= 0; j --)
            for (int k = 1; k <= s[i]; k ++) // 这样保证只会拿一个
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m] << endl;
    return 0;
}

5. 混合背包

我们可以把 $01$ 背包看成每个物品数量都为 $1$ 的多重背包，然后将多重背包和完全背包分成两类做。

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) {
        int v, w, s;
        cin >> v >> w >> s;
        if (s == 0) {
            for (int j = v; j <= m; j ++)
                f[j] = max(f[j], f[j - v] + w);
        } else {
            if (s == -1) s = 1;
            for (int k = 1; k <= s; k *= 2) {
                for (int j = m; j >= v * k; j --)
                    f[j] = max(f[j], f[j - v * k] + w * k);
                s -= k;
            }
            if (s)
                for (int j = m; j >= v * s; j --)
                    f[j] = max(f[j], f[j - v * s] + w * s);
        }
    }
    cout << f[m] << endl;
    return 0;
}

6. 二维费用的背包

也是 $01$ 背包的思路，只不过在 $01$ 背包的 $f$ 数组上再加一维重量，具体的：$f_{j,k} = \max(f_{j, k}, f_{j - v_i, k - m_i} + w)$

#include <iostream>
using namespace std;
const int N = 1010, M = 110;
int n, m1, m2;
int f[N][N];
int main() {
    cin >> n >> m1 >> m2;
    for (int i = 1; i <= n; i ++) {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for (int j = m1; j >= v1; j --)
            for (int k = m2; k >= v2; k --)
                f[j][k] = max(f[j][k], f[j - v1][k - v2] + w);
    }
    printf("%d\n", f[m1][m2]);
    return 0;
}

7. 有依赖的背包

物品的依赖关系连成一棵树，所以考虑树形 $DP$。

这道题中我们不能使用原来背包状态转移的思路，原来的思路是第 $i$ 件物品依赖第 $i - 1$ 件物品，辐射到这题树形 $DP$ 中就是要枚举子树的所有组合，可能会达到 $2 ^ k$ 次方的级别，所以我们要改变状态设计思路。

接下来是 $DP$ 思路。

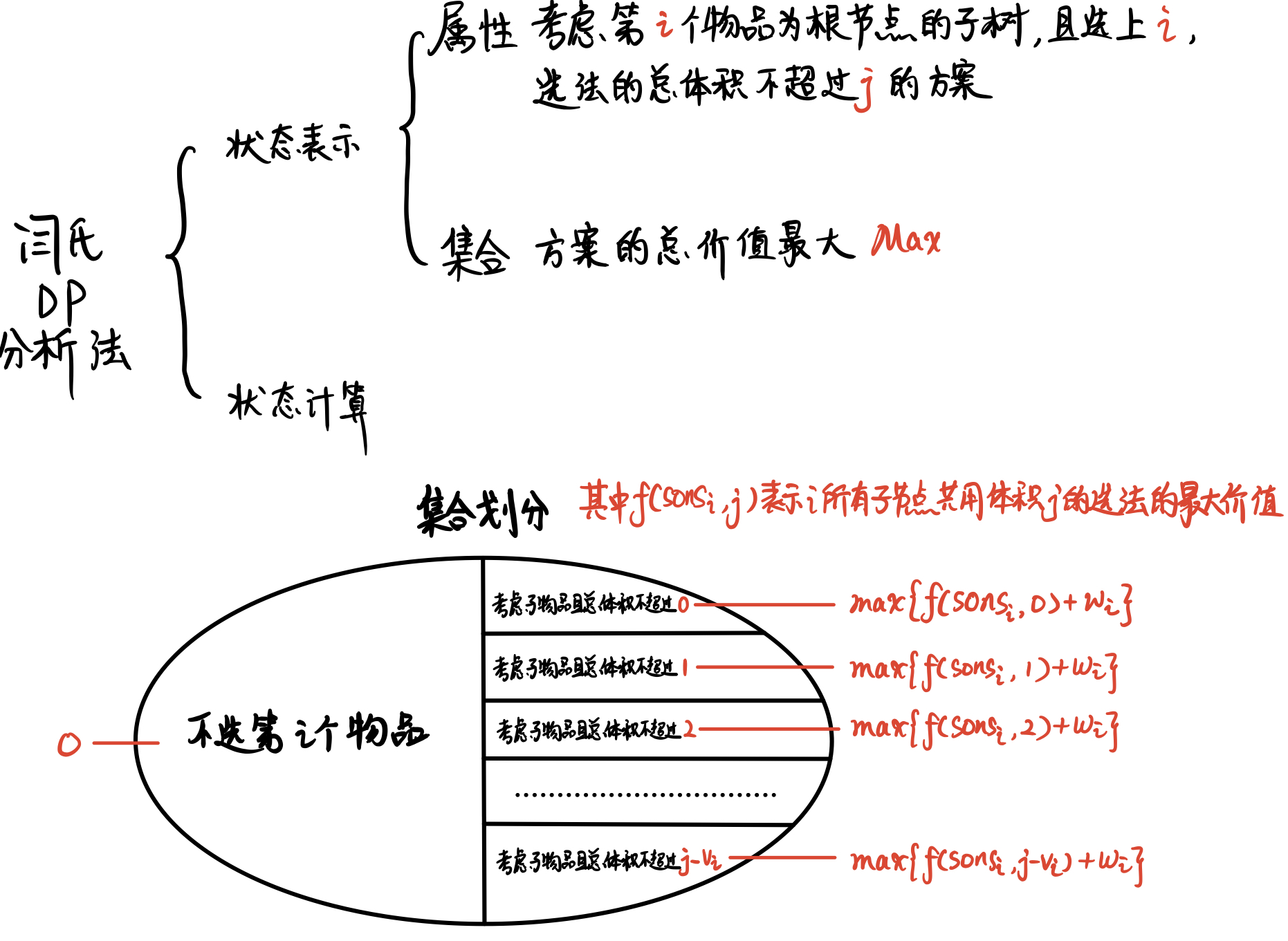
笔者觉得这张图（作者：一只野生彩色铅笔）画的很清晰，就拿来一用。

具体操作过程详见注释。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 110;
int n, m;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u) {
    // 枚举 u 的儿子
    for (int i = h[u]; ~i; i = ne[i]) {
        int son = e[i];
        // 先求出儿子再求父亲
        dfs(e[i]);
        // 由于我们一定要选点 u，所以总体积要先减去 u 的体积
        for (int j = m - v[u]; j >= 0; j --)
            for (int k = 0; k <= j; k ++) // 枚举 son 需要消耗的体积
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
    }
    // 由于我们做的时候先忽略了 u，所以现在要再把 u 加回来
    for (int i = m; i >= v[u]; i --) 
        f[u][i] = f[u][i - v[u]] + w[u];
    // 如果连 u 都装不下那就不合法
    for (int i = 0; i < v[u]; i ++)
        f[u][i] = 0;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    int root;
    for (int i = 1; i <= n; i ++) {
        int p; cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p, i);
    }
    dfs(root);
    cout << f[root][m] << endl;
    return 0;
}

8. 求方案数

考虑在 $01$ 背包模型的基础上再加上 $g$ 数组来记录方案数。

状态表示：

  • 集合：考虑前 $i$ 个物品，当前已使用的体积恰好是 $j$，且价值最大的方案
  • 属性：$Sum$

状态转移：

  1. 若$f_{i, j} = f_{i - 1,j}$ 并且 $f_{i, j} = f_{i - 1, j - v_i} + w_i$，则$g_{i, j} = g_{i - 1,j} + g_{i - 1, j - v_i}$
  2. 若$f_{i, j} \ne f_{i - 1,j}$ 并且 $f_{i, j} = f_{i - 1, j - v_i} + w_i$，则$g_{i, j} = g_{i - 1, j - v_i}$
  3. 若$f_{i, j} = f_{i - 1,j}$ 并且 $f_{i, j} \ne f_{i - 1, j - v_i} + w_i$，则$g_{i, j} = g_{i - 1, j}$

初始状态：$g_{0,0} = 1$

由于我们 $g$ 数组的定义是恰好，而题目要求不超过，所以要再走一遍循环。（当然你也可以直接把 $g$ 定义成不超过，会简单一些）。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010, Mod = 1e9 + 7;
int n, m;
int v[N], w[N];
int f[N][N], g[N][N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    g[0][0] = 1;
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++) {
            if (f[i][j] == f[i - 1][j]) g[i][j] = (g[i][j] + g[i - 1][j]) % Mod;
            if (j >= v[i] && f[i][j] == f[i - 1][j - v[i]] + w[i]) 
                g[i][j] = (g[i][j] + g[i - 1][j - v[i]]) % Mod;
        }
    int res = 0;
    for (int i = 0; i <= m; i ++)
        if (f[n][i] == f[n][m])
            res = (res + g[n][i]) % Mod;
    printf("%d\n", res);
    return 0;
}

9. 求具体方案

由于题目要求从小到大输出，所以我们的 $DP$ 要倒序 $DP$，而要求路径，其实只要满足 $f_{i, j} = f_{i - 1, j - v_i} + w_i $，那便可以加入路径中。原因是当我们在分叉转移时，如果 $f_{i, j} = f_{i - 1, j - v_i} + w_i = f_{i - 1, j}$ 时，为了保证字典序最小，我们势必一定要选上这个物品，所以只要考虑一个条件即可。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m, cnt;
int v[N], w[N], f[N][N], p[N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
    for (int i = n; i; i --)
        for (int j = 0; j <= m; j ++) {
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) 
                f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    for (int i = 1, j = m; i <= n; i ++) 
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
            p[++ cnt] = i, j -= v[i];
    for (int i = 1; i <= cnt; i ++) 
        printf("%d ", p[i]);
    return 0;
}

写在最后

背包问题实际上就是那几个模型改来改去，出了单调队列优化和树形 $DP$ 之外的其实毫无难点，所以最关键的是把 $01$ 和完全背包理解清楚，之后的题就很好理解了。

最后的最后

这只是最基础的模板，具体使用还得根据实际进行修改。

9 评论

用户头像
Conan15   1个月前      1    踩      回复

01 背包的属性 最大值 $Max$ 为什么要居中显示（）
还有为什么不用 \max $\max$

用户头像
Conan15   1个月前         踩      回复
  1. 完全背包
    标题的上一行那里为什么公式中间还能用顿号（）（）$f_{1、2、3、4}$
用户头像
Conan15   1个月前    回复了 Conan15 的评论         踩      回复

我已经一年半没给学弟讲题了 /xk

用户头像
天元之弈   1个月前    回复了 Conan15 的评论         踩      回复

谢谢柯南qwq

用户头像
天元之弈   1个月前    回复了 Conan15 的评论         踩      回复

一看洛谷题解就经常被退回

用户头像
天元之弈   1个月前    回复了 Conan15 的评论         踩      回复

Typora的编辑和AcWing的好像不一样，复制过来就会有格式错误

用户头像
天元之弈   1个月前    回复了 Conan15 的评论         踩      回复

我们学校的学弟还要人讲 A+B

用户头像
Conan15   1个月前         踩      回复

前排。

用户头像
Conan15   1个月前         踩      回复

讲的很好啊 awa