返回上一级检索目录 《背包模型》

未完待续 Updating......

完全背包问题

问题

有$N$件物品和一个容量是$V$的背包。每种物品都有无限件可用。
第$i$件物品的体积是$v_i$，价值是$w_i$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

分析

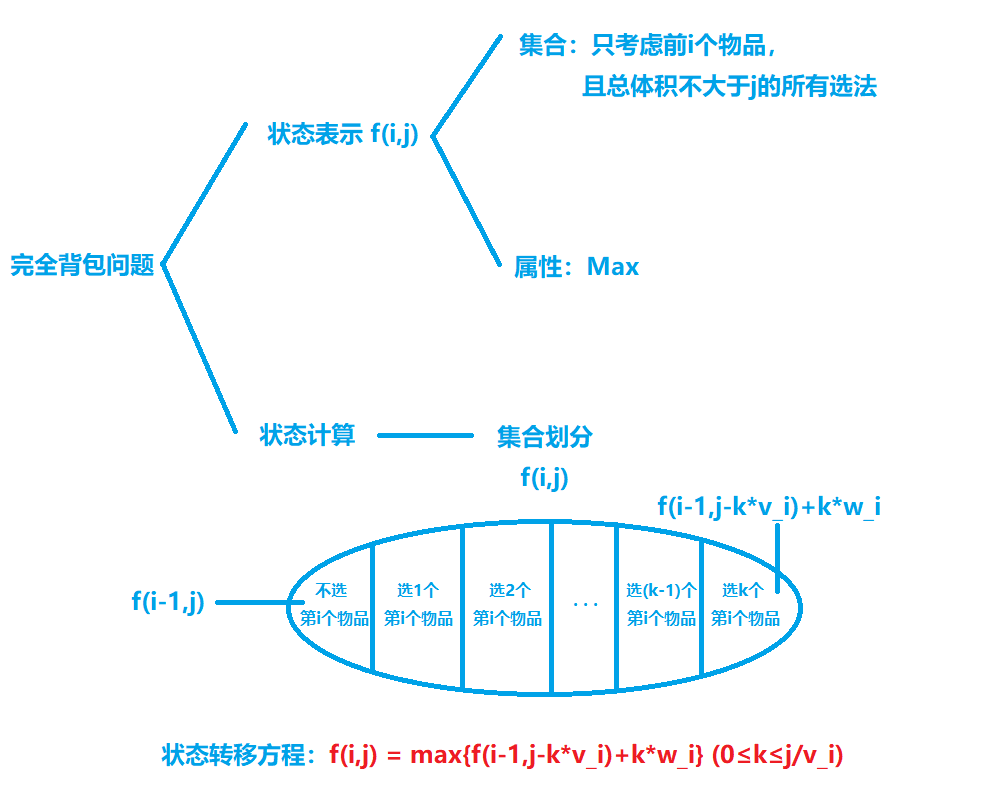
状态转移方程
$$ f[i,j] = \max_{k=0}^{\lfloor \frac{j}{v_i} \rfloor}\{f[i-1,j-k \times v_i]+k \times w_i\} $$

代码模板

朴素版

for (int i=1; i<=n; i++) {
    for (int j=1; j<=m; j++) {
        for (int k=0; k*v[i]<=j; k++) {
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
        }
    }
}

优化版

$\because f(i,j) = \max(f(i-1,j),f(i-1,j-v_i)+w_i,f(i-1,j-2v_i)+2w_i,\dots,f(i-1,j-kv_i)+kw_i)$
$f(i,j-v_i) = \max(f(i-1,j-v_i),f(i-1,j-2v_i)+w_i,\dots,f(i-1,j-kv_i)+(k-1)w_i)$
$\therefore f(i,j) = \max(f(i-1,j),f(i,j-v_i)+w_i)$

for (int i=1; i<=n; i++) {
    for (int j=1; j<=m; j++) {
        f[i][j] = f[i-1][j];
        if (j >= v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
    }
}

滚动数组优化

for (int i=1; i<=n; i++) {
    for (int j=v[i]; j<=m; j++) {
        f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
}