本篇主要以总结为主 较有基础食用更加
背包问题复习题单讲解
目录
1.什么是背包问题
2.背包问题的分类
3.背包问题的初始化问题
4.背包问题的优化
5.背包问题的演变
6.背包问题真题详解
1. 什么是背包问题
$\space\space\space\space\space$ 背包问题 不同于线性dp的纯线性动态改变问题 背包问题更多的是基于某项限制下的最优问题 在dp中 我们知道阶段 决策 状态 是动态规划的三要素 而子问题重叠性 无后效性 最优子结构性质是求解动态规划的三个基本条件 这些在本文不在赘述
$\space\space\space\space\space$ 这里我们略微涉及下 状态转移 (引入一句话) 一个正确的状态转移方程的求解过程遍历了所有可用的策略 也就覆盖了问题的所有方案 更多的动态规划更多的像一个暴力搜索算法 只不过是基于启发式搜索的前提下 使得搜索的范围局限于题目所询问的范围之内
$\space\space\space\space\space$ 背包问题的询问往往是基于体积和价值两个维度 在体积的限制下对每一个物品进行01决策 进而求价值的最大
2.背包问题的分类
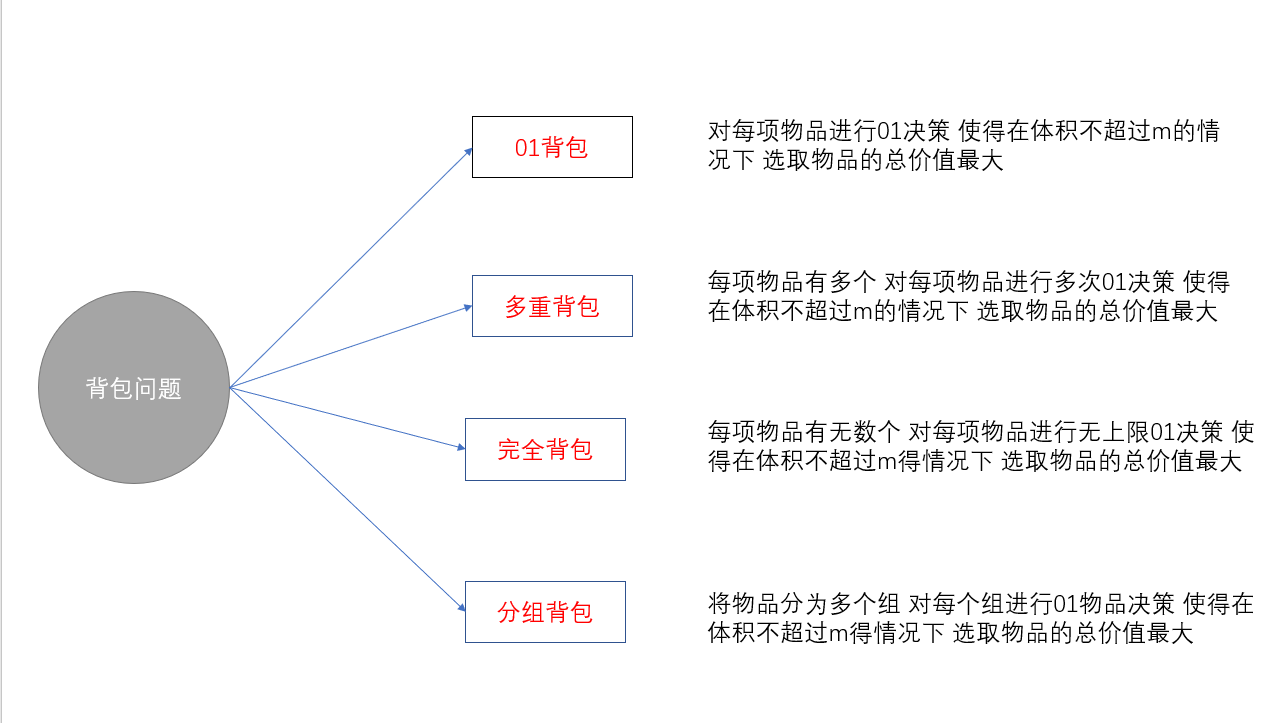
2.1 01背包
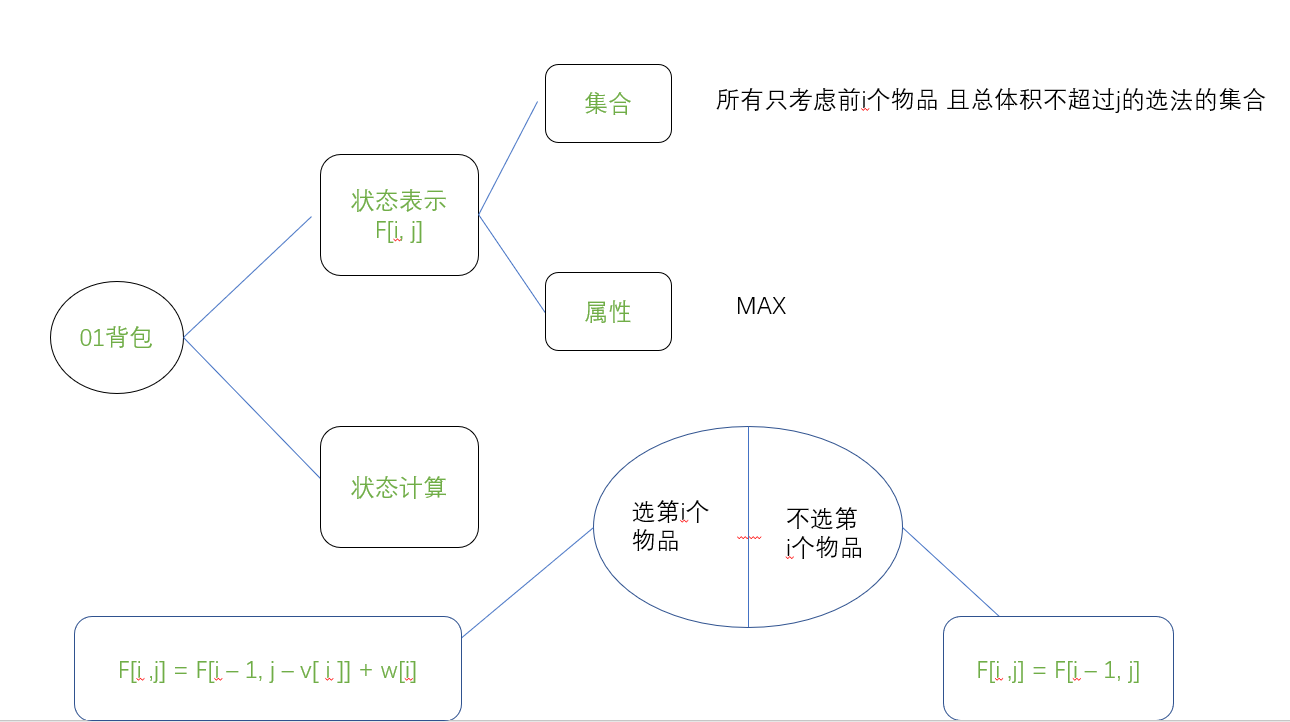

for(int i = 1; i <= n; i ++)
{
for(int j = 0; j <= m; j ++)
{
f[i][j] = f[i - 1][j]; //继承
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); //转移
}
}
滚动数组优化后
for(int i = 1; i <= n; i ++)
{
for(int j = m; j >= v[i]; j --)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
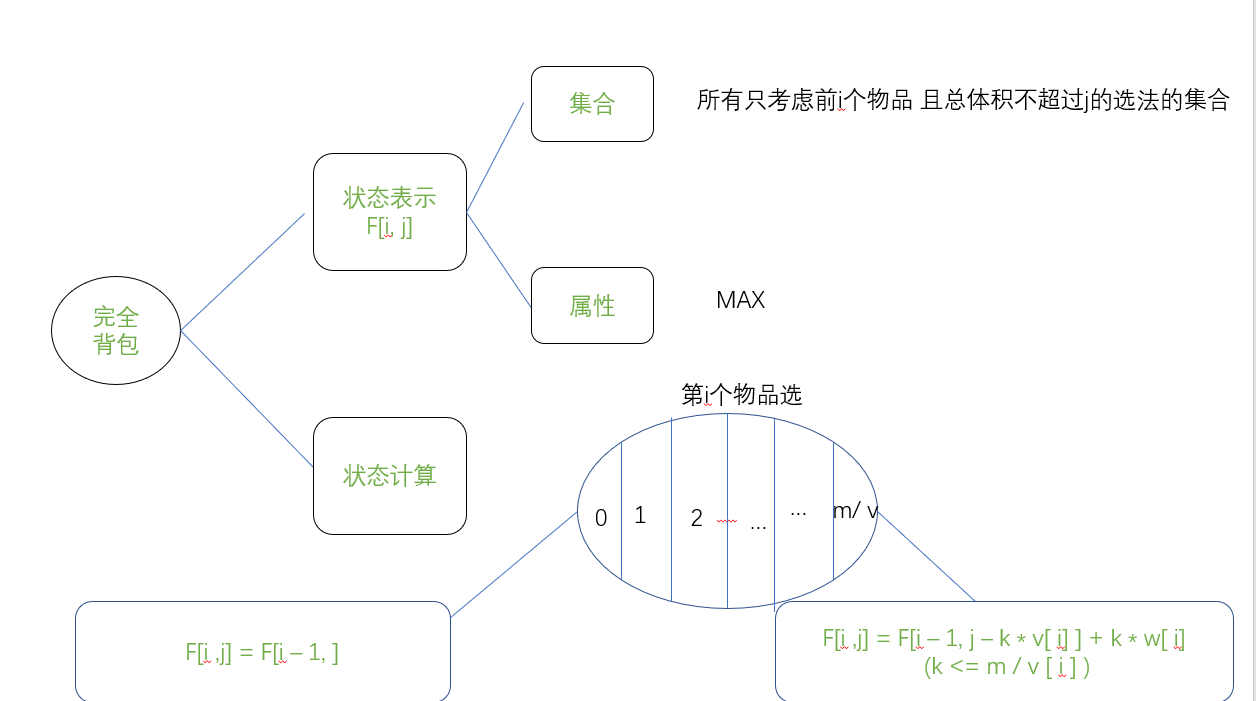
2.2 完全背包
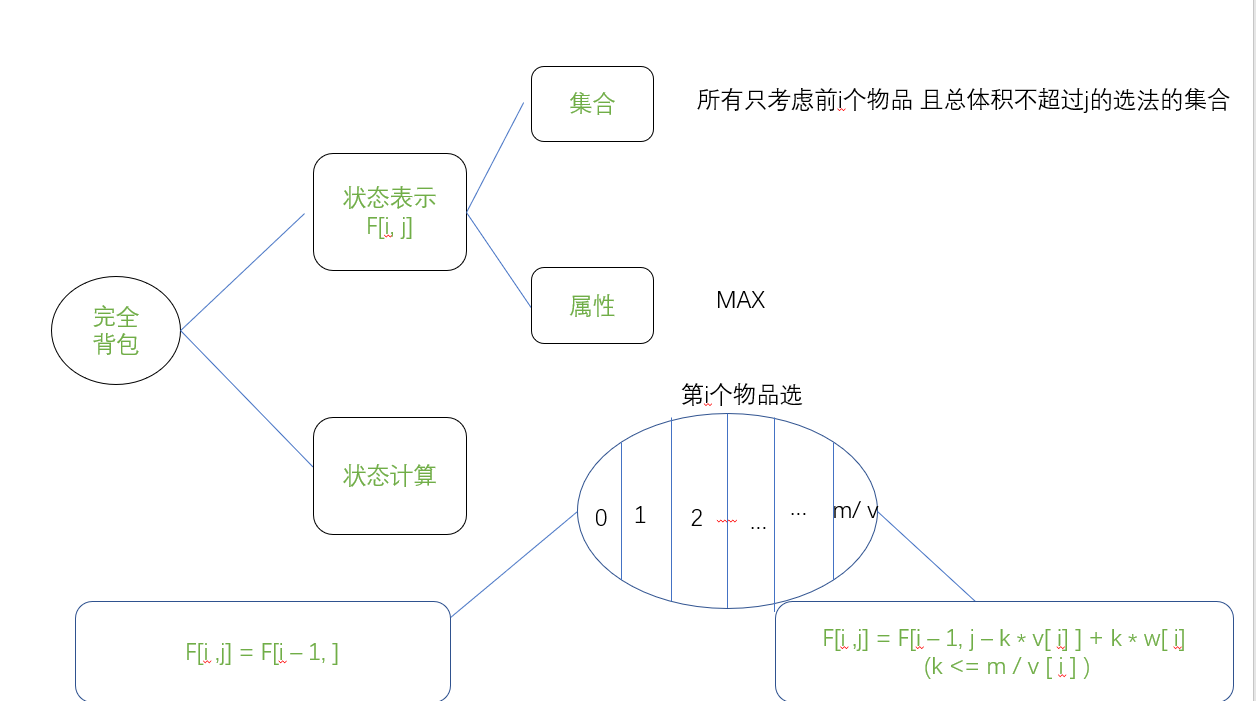

朴素版
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j <= m; j ++)
{
for(int k = 0; k <= j / v[i]; k ++)
{
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
滚动数组优化后
for(int i = 1; i <= n; i ++)
{
for(int j = v[i]; j <= m; j ++)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
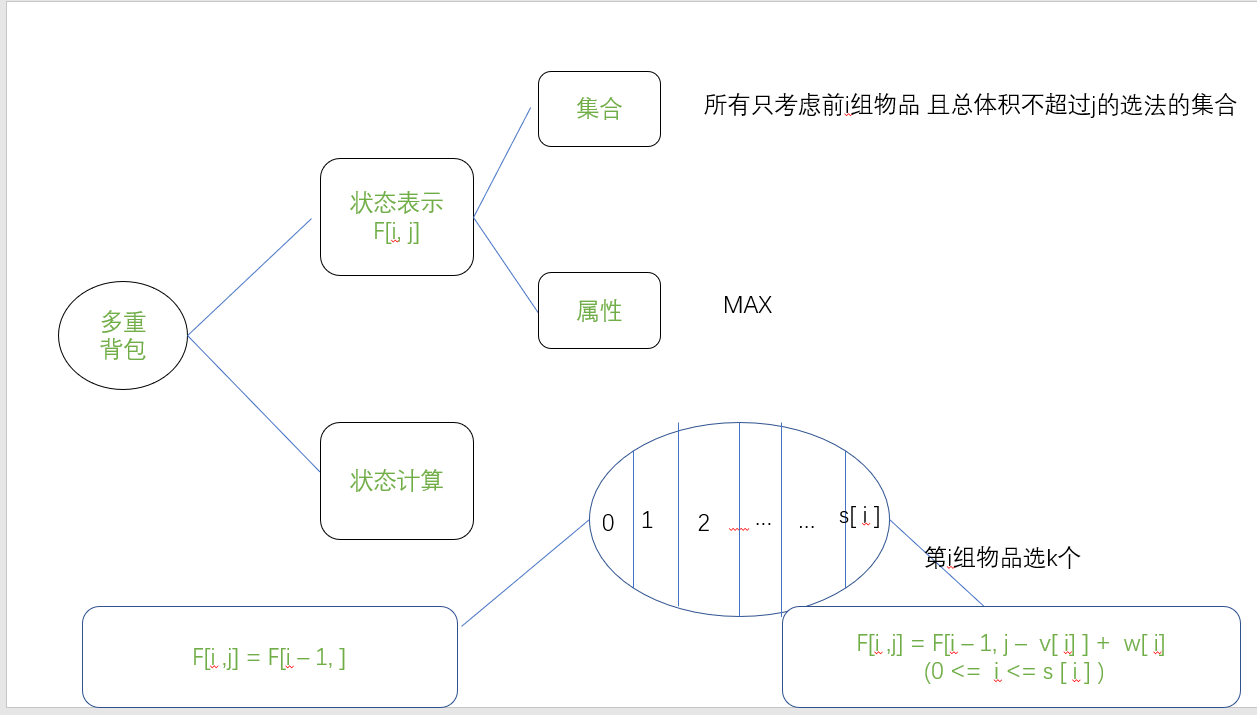
2.3 多重背包


for(int i = 1; i <= n; i ++)
{
for(int j = 0; j <= m; j ++)
{
for(int k = 0; k <= s[i] && k * v[i] <= j; k ++)
{
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
cout << f[n][m] << endl;
滚动数组优化
for(int i = 1; i <= n; i ++)
{
for(int j = m; j >= v[i]; j --)
{
for(int k = 0; k <= j / v[i] && k <= s[i]; k ++)
{
f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
}
}
}
cout << f[m] << endl;
二进制优化
for(int i = 1; i <= n; i ++) // 二进制拆分成01背包
{
cin >> a >> b >> s;
int k = 1;
while(k <= s)
{
cnt ++;
v[cnt] = k * a;
w[cnt] = k * b;
s -= k;
k *= 2;
}
if(s > 0)
{
cnt ++;
v[cnt] = s * a;
w[cnt] = s * b;
}
}
n = cnt;
for(int i = 1; i <= n; i ++)
for(int j = m; j >= v[i]; j --)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
单调队列优化
2.4 分组背包

for(int i = 1; i <= n; i ++)
{
int s;
cin >> s;
for(int i = 1; i <= s; i ++)
cin >> v[i] >> w[i];
for(int j = m; j >= 0; j --)
{
for(int k = 1; k <= s; k ++)
if(j >= v[k]) f[j] = max(f[j], f[j - v[k]] + w[k]);
}
}
cout << f[m];
3.背包的初始化 - 小呆呆
dp初始化 为0代表这个点是存在 可以由这个点而更新 而初始成极值 代表这个这个点不存在 没有实际意义

5.背包的演变
该类型的考法有
1.统计方案数
2.输出字典序最小的最优方案
3.求次优解或第k优解

