目录

对邻接表存图的一些理解

图论的基础是建图，而建图也是图论难题中最难的部分。在我们最常用的两种建图方式中，邻接表 的难度远远比 邻接矩阵 大。我这篇分享就是来聊聊我自己对邻接表的看法。（不会邻接矩阵的请调头）

邻接表是干嘛的

不是说了吗，建图
邻接表是用来存 稀疏图 的。在稀疏图中，邻接矩阵会浪费大量空间，导致MLE。邻接表就能解决这个问题。

设图中点数为 $n$，边数为 $m$：
稠密图是 $m$ 在 $n^2$ 级别的图，稀疏图是 $m$ 在 $n$ 级别的图。

提示一句：接下来的内容需要链表，没学过请先学，学过可以放心食用。

邻接表的原理

这一部分我会按自己理解给大家讲讲邻接表。非喜勿喷

• 还是设图中点数为 $n$，边数为 $m$。
• 邻接矩阵的空间复杂度为 $O(n^2)$，与 $n$ 直接相关。
• 但如果我们要存稀疏图，因为稀疏图中 $m$ 较小，所以我们要让空间复杂度 与 $m$ 相关。
• 而且这个复杂度必须小于邻接矩阵的 $O(n^2)$。
• 所以新方法的空间复杂度应为 $O(m)$。是 线性 的。
• 那如何才能通过常数个一维数组建图呢？
• 考虑一下我们是如何输入一个图的。
• 输入的每条边都是由 父节点 $(a)$ 、子节点 $(b)$ 和 边权 $(c)$ 组成的。
• 所以我们可以开三个数组x[n],y[n],w[n]来存这些信息，并用下标idx把它们关联起来。（也可以用结构体）
• 至此，我们其实已经实现了 空间复杂度为 $O(m)$ 的建图（是不是与你想象的完全不同？）
• 代码如下：（这儿就不配图了，因为我懒）

void add(int a,int b,int c)
{
    x[idx]=a;
    y[idx]=b;
    z[idx]=c;
    idx++; //初始为0
    return;
}

• 接下来让我们考虑优化。
• 首先，我们要明确我们的优化方向。
• 很明显，我们大多数时候遍历图都是从一个已知点来寻找子节点（像 $Dijkstra$ 算法）或一口气遍历所有边（像 $Bellman-Ford$ 算法）。
• 而后者我们已经可以轻松实现。
• 所以我们要想办法优化 从一个已知点来寻找子节点 的时间复杂度。
• 这里我们就可以用 链表的思想，即多开一个ne数组来 指向下一条与这条边父节点相同的边。如图：

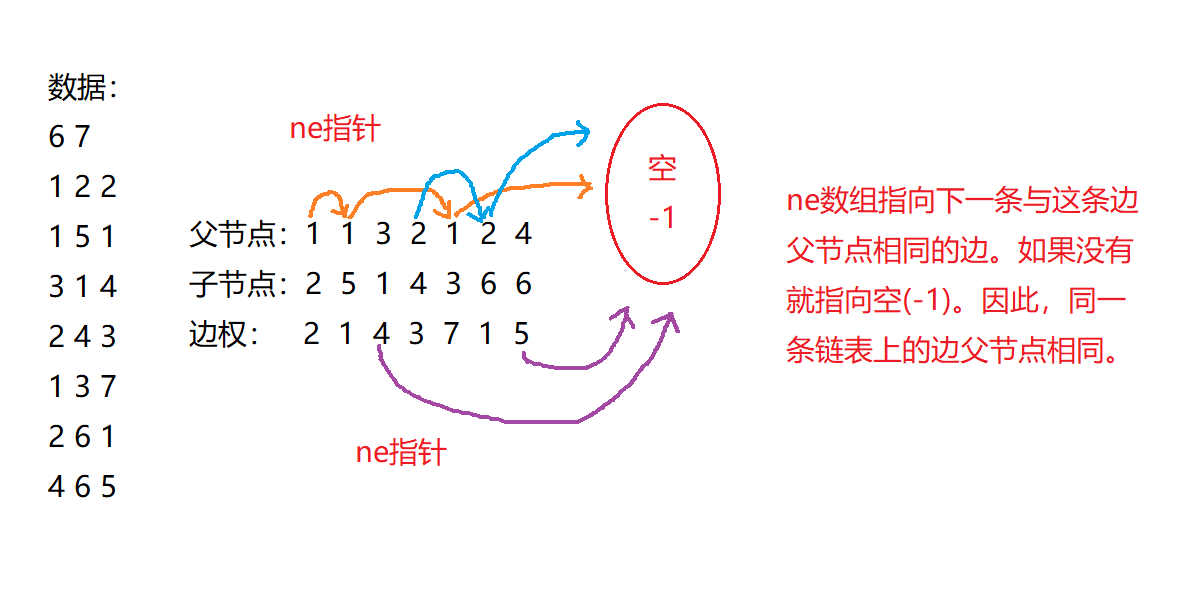
• 遍历一个已知点的子节点时就可以用链表的方法 i=ne[i] 啦！
• 诶，等一下，我们都从一个已知父节点来寻找子节点了，为什么还要开数组存父节点呢？

• 我们可以不用父节点数组。

• 再看看我们的思路有没有漏洞。

• 循环的时候，$i$ 的初值是多少呢？
• 用现有的数据，我们很难确定。
• 那我们就再开一个数组h[n]，来记录 每一个点作为父节点的第一条边（初始为 -1）。如图：

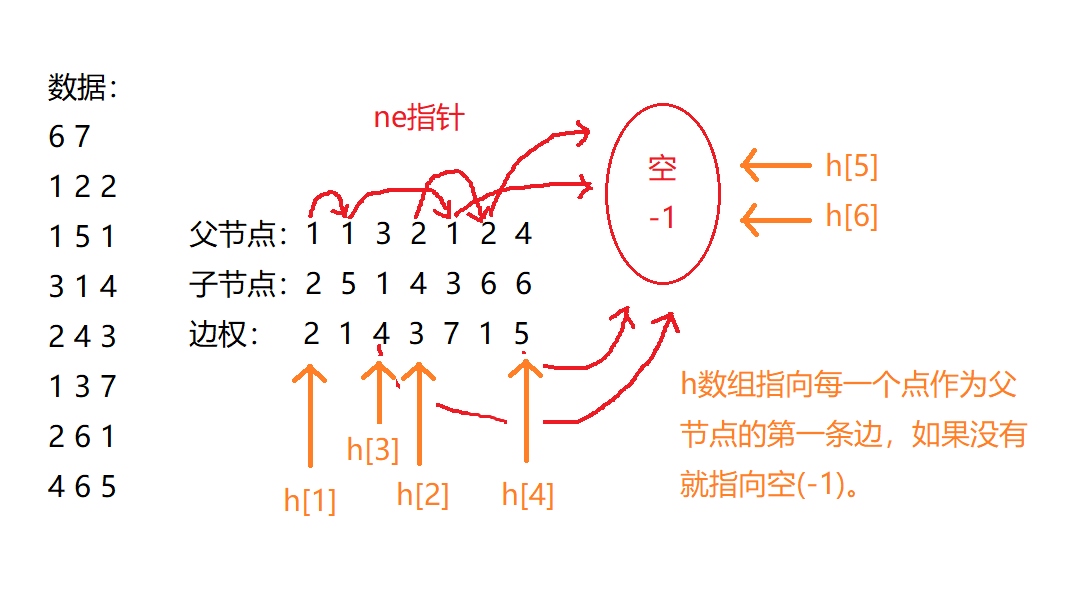
• 再考虑一下add函数中有没有问题。
• 按上面的思路，我们会用 尾插法，即在链表尾部插入元素。
• 但我们怎么知道链表的尾部在哪里呢？总不能再开个数组吧。
• 又注意到 链表 其实是可以 无序的，因为遍历时不要求顺序。
• 所以我们可以采用 头插法，即在链表头部插入元素。如图：

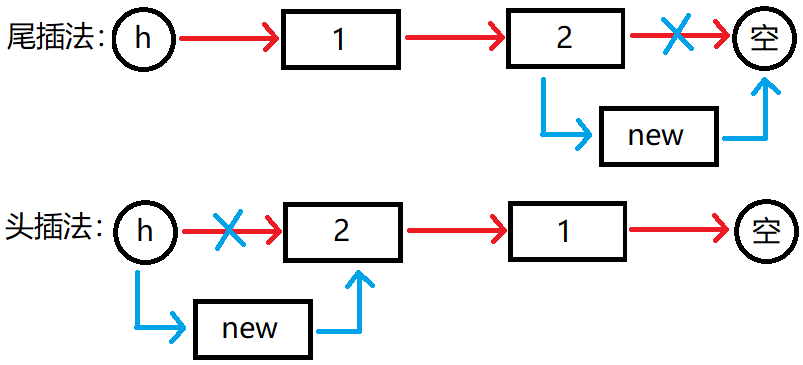
• 具体的做法就是先设置ne指针ne[idx]=h[a]（a就是父节点），再改头部元素h[a]=idx（前后顺序不能反）。

$(update\ 2022.4.20)$：以上是邻接表存图的一个要点。理解邻接表存图的另一个要点是想清楚h和ne组成的链表的每一个元素值要存的是图中边的信息，而不是用h和ne两个指针来从父节点指向子节点。

上代码

void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx; //h初始为空(-1)
    idx++; //初始为0
    return;
}

附：各数组下标和值的意义

e[公共下标]=子节点编号
w[公共下标]=边权
ne[公共下标]=公共下标 
h[点的编号]=公共下标